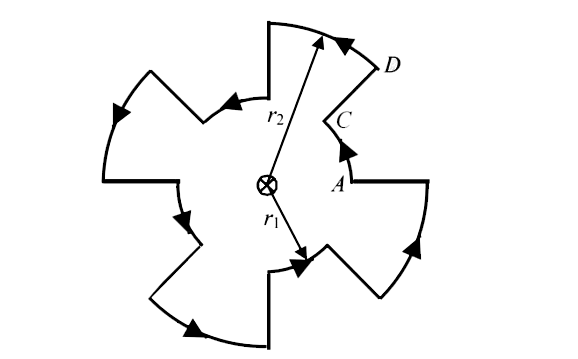
A current of 10A flows around a closed path in a circuit which is in horizontal plane as shown in the figure . The circuit consists of eight alternating arcs of radiir1=0.08mandr1=0.12m.Eacharc⊂tendsthesameathecenter.<br>(a)F∈dthemag≠tixcfield∏ucedbythis∘uitatthecenter.<br>(b)An∈f∈itelylongstraightwirecarry∈gacurrentof10 Aispassingthroughthecenteroftheabove∘uitverticallywiththedirectionofthecurrentbe∈g∫othepla≠ofthe∘uit.Wˆistheforceact∈gonthearcACandthestraightsegment CD due to the current at the center?
The correct Answer is:(i) 6.54 (ii) (0, 8.1)
(i) 6.54 (ii) (0,8.1)
(i) Given i=10A,r1=0.08m and r2=0.12m. Straight portion i.e. CD etc., will produce zero magnetic field at the centre. Rest eight arcs will produce the magnetic field at the centre in the same direction i.e., perpendicular to the paper outwards or vertically upwards and its magnitude is
B=Binnerarcs+Bouterarcs
=12{μ0i2r1}+12{μ0i2r2}=(μ04π)(πi)(r1+r2r1r2)
Substituting the values we have
B=(10−7)(3.14)(10)(0.08+0.12)(0.08×0.12)
B=6.54×10−5T
(vertically upward or outward normal to the paper)
(ii) Force on AC
Force on circular portions of the circuit i.e., AC etc, due to the wire at the centre will be zero because magnetic field due to the central wire at these arcs will be tangential θ=180∘.
Force on CD
Current in central wire is also i=10A. Magnetic field at distance x due to central wire
B=μ02π.ix∴ Magnetic force on element dx due to this magnetic field
dF=(i)(μ02π.ix).dx=(μ02πi2dxx,(F=ilBsin90∘)
Therefore net force on CD is
F=∫x=r2x=r1dF=μ0i22π∫0.120.08dxx=μ02πi2In(32)
Substituting the values F=(2×10−7)(10)2In(1.5) or F=8.1×10−6N (in wards)
Force on wire at the centre, Net on wire at the centre
Net magnetic field at the centre due to the circuit is in vertical direction and current in the wire in centre is also in vertical direction. Therefore, net force on the wire at the centre will be zero. (θ=180∘). Hence,
(i) force acting on the wire at the centre is zero (ii) force on arc AC=0
(iii) force on segment CD is 8.1×10−6N (inwards)
Similar Questions
A current of 10A flows around a closed path in a circuit which is int eh horizontal plne as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
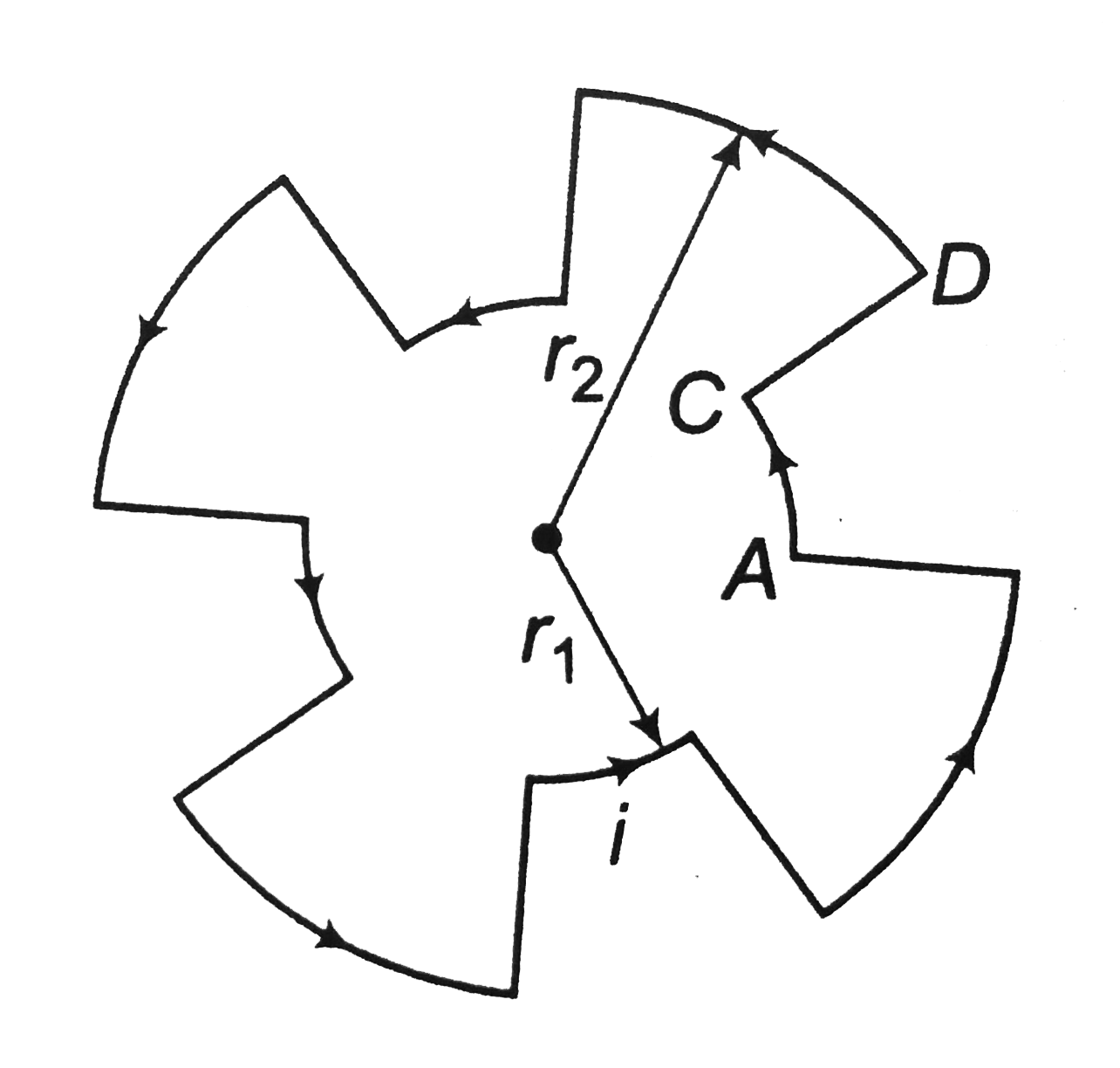
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centredue to the curren in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
View SolutionA current of 4A flows around a circuit for 10s. How much charge flows past a point in the circuit in this time?
View Solution
Knowledge Check
A current I flows around a closed path in the horizontal plane of circle as shown in the figure The path consists of eight arcs with alternating radii r and 2r . Each segment of arc subtends equal angle at the common centre P The magnetic field produced by current path at point P is
 .A38μ0Ir , perpendicular to the plane of the paper and directed inward .B38μ0Ir , perpendicular to the plane of the paper and directed outward .C38μ0Ir , perpendicular to the plane of the paper and directed inward .D38μ0Ir , perpendicular to the plane of the paper and directed outward .
.A38μ0Ir , perpendicular to the plane of the paper and directed inward .B38μ0Ir , perpendicular to the plane of the paper and directed outward .C38μ0Ir , perpendicular to the plane of the paper and directed inward .D38μ0Ir , perpendicular to the plane of the paper and directed outward .In the circuit shown in figure current in the circuit is
 A1.27AB2.23AC4.26AD4 A
A1.27AB2.23AC4.26AD4 AIn the figure shown, a current of 2 amperes flows in the circuit. The impedence of the circuit is-
 A170ΩB70ΩC130ΩD120Ω
A170ΩB70ΩC130ΩD120Ω
In a circle of radius 28 cm, an arc subtends an angle of 108∘ at the center. Find the length of the arc.
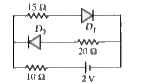
View SolutionThe current flowing through 10Ω resistor in the circuit shown in the figure is
View SolutionShown in the figure is an R−L circuit. Just after the key (K) is closed

View SolutionA current of 10A is flowing in a equilateral triangle of side length l=1M as shown in figure. The magnetic field at center of triangle is:
_2019_CBT6_E01_040_Q01.png)
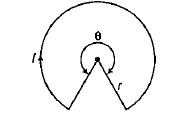
View SolutionA current I ampere flows in the loop having circular arc of radius r metre subtending an angle 6 as shown in figure. The magnetic field, at center of circle is
View Solution
