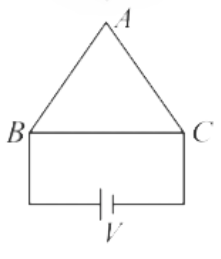
An equilateral triangle ABC of side length a is made. The sides AB and AC have resistance per unit length β, and side BC has resistasnce per unit length 2β. An ideal battery of EMF V is now connected across BC as shown. The magnetic field intensity at the centrroid of the triangle ABC is n(μ0V4πβa2), then the value of n is _______. (Consider only the field due to sides AB, BC and AC of the triangle, and neglect the field due to other wires)
Video Solution
Text Solution
The correct Answer is:3
RBAC=β(2a)=2βa,RBC=2β(a)=2βa⇒IBAC=I−V2β,IBc=I=V2β
Field at centroid due to AB , B0=μ0I4π(a2√3)(sin+60∘+sin60∘)
B0=3μ0I4πa (into the plane), Net field at centroid =2B0−B0,=B0=3μ0V4πβa2
|
Similar Questions
Knowledge Check
In an equilateral triangle ABC of side 10cm, the side BC is trisected at D. Then the length (in cm) of AD is
A3√7B7√3C10√73D7√103In an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2DNone of theseIn an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2Dnone of these
If the mid points of the sides AB and AC of a triangle ABC are (3, 5), (-3,-3) then the length of the side BC is
View SolutionIn a triangle ABC the length of the sides, AB is 3 m and BC is 5 m what is the length of AC, if the angle formed at B is 60∘
View SolutionA current of 10A is flowing in a equilateral triangle of side length l=1M as shown in figure. The magnetic field at center of triangle is:
_2019_CBT6_E01_040_Q01.png)
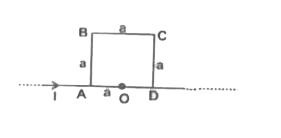
View SolutionThe resistance per unit length of the wires in segments AB, BC, CD, and AD are the same. The magnetic field due to the current at point O is
View SolutionAn isoceles right triangl ABC has an incircle with centre O, which touches the sides AB, BC, and AC . Find radius of circle
View Solution
