The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

(CK1K2K2−K11nK2K1,) let length of breath of the capacitor be /and b respectively and be the distance between the plates as shown figures then, consider a strip at a distance x if widh dx.
Now, QR=xtanθandPQ=d−xtanθ
Where tanθ=d/1, capacitor of PQ
C1=K1ε0(bdx)d−xtanθ=K1ε0(bdx)d−xd1
C1=K1εb/dxd(1−x)=K1ε0A(dx)d(1−x)andC1=capicitor of QR=K2ε0b(dx)xtanθ
C1=K2ε0A(dx)xd(tanθ=d1)
Now C1 and C2 are in series.Therefore,their resultant capacity C0 will be given by 1C0=1C1+1C2
Then 1C0=1C2+1C2=d(1−x)K1ε0A(dx)+xdK2ε0A(dx)1c0=dε0A(dx)(1−xK1+xk2)=d{K2(1−x)+K1x}ε0AK1K2(dx)
C0=ε0AK1K2D{K2(1−x)+K1x}dx,C0=ε0AK1K2d{K2I+(K1=K2)x}dx
Now, the net capacitance of the given parallel plate capacitor is obtained by adding such infinitesimal capacitors placed parallel from x=0 to x=1
i.e., Finally we get Cn=K1K2A(K2_K1)dln(K2)K1=CK1K2K2−K1ln(K2)kK1, where C=ε0Ad.

Similar Questions
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionFind out the capacitance of parallel plate capacitor of plate area A and plate separation d.
View Solution
Knowledge Check
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)To reduce the capacitance of parallel plate capacitor, the space between the plate is
Afilled with dielectric materialBreduce and area of the plates is increasedCincreased and area of the plates is decreasedDincreased and area is increased relativelyA parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be
 A∈0Ad(∈1+∈2)B∈0Ad(∈1+∈2)∈1∈2C2∈0Ad∈1∈2(∈1+∈2)D2∈0Ad(∈1+∈2)∈1∈2
A∈0Ad(∈1+∈2)B∈0Ad(∈1+∈2)∈1∈2C2∈0Ad∈1∈2(∈1+∈2)D2∈0Ad(∈1+∈2)∈1∈2
The area A of a parallel plate capacitor is divided into two equal, halves and filled with two media of dielectric constants K1andK2 respectively. The capacitance of the capacitor will be

View SolutionFig shows a parallel plate capacitor of plate area A and plate separation d. Its entire space is filled with three different dielectric slabs of same thickness. Find the equivalent capacitance of the arrangment.
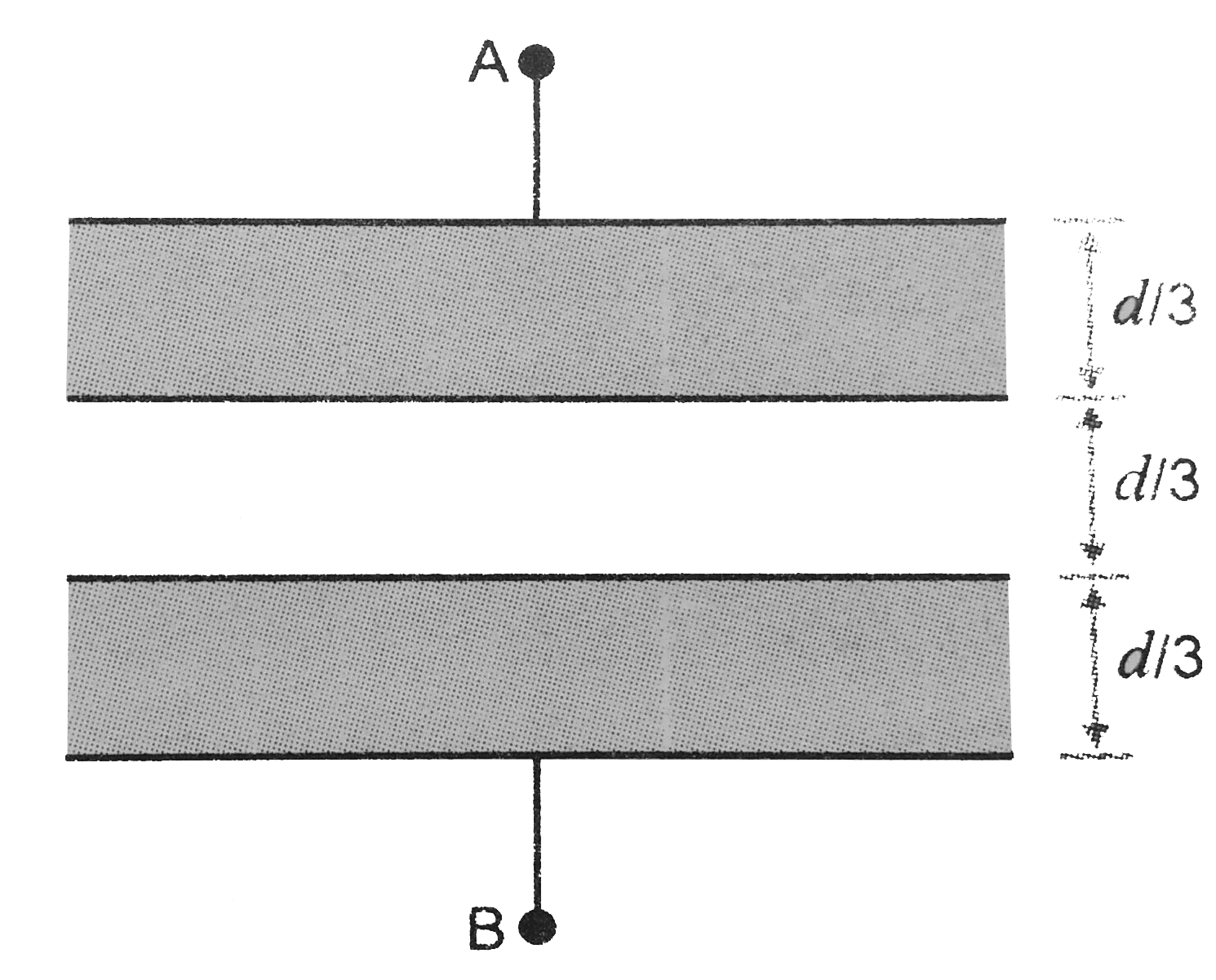
View SolutionA parallel-plate capacitor with plate area A has separation d between the plates. Two dielectric slabs of dielectric constant K1 and K2 of same area A/2 and thickness d/2 are inserted in the space between the plates. The capacitance of the capacitor will be given by :
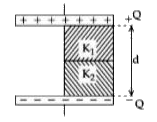
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

View Solution
