A capacitor of capacitance $1 μ F$ is connected in parallel with a resistance $10 Ω$ and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance $1 Ω$ . The potential difference across the capacitor at steady state is (in Volt)

A

$\frac{50}{11}$

B

$\frac{100}{11}$

C

$\frac{250}{11}$

D

$\frac{500}{11}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:D

To find the potential difference across the capacitor at steady state, we can follow these steps:
Step 1: Understand the circuit configuration
We have a capacitor (1 µF) in parallel with a resistor (10 Ω). This combination is connected to a battery with an EMF of 50 V and an internal resistance of 1 Ω.
Step 2: Calculate the total resistance in the circuit
The total resistance in the circuit is the sum of the internal resistance of the battery and the resistance in parallel with the capacitor. The total resistance $R_{t o t a l}$ can be calculated as:
$R_{t o t a l} = R_{i n t e r n a l} + R_{p a r a l l e l}$
Where $R_{p a r a l l e l}$ is the equivalent resistance of the resistor in parallel with the capacitor. Since the capacitor behaves like an open circuit at steady state, we only consider the resistor:
$R_{p a r a l l e l} = 10 Ω$
Thus,
$R_{t o t a l} = 1 Ω + 10 Ω = 11 Ω$
Step 3: Calculate the total current in the circuit
Using Ohm's law, the total current $I$ flowing through the circuit can be calculated as:
$I = \frac{V_{b a t t e r y}}{R_{t o t a l}} = \frac{50 V}{11 Ω} \approx 4.545 A$
Step 4: Calculate the voltage drop across the resistor
The voltage drop $V_{R}$ across the internal resistance of the battery can be calculated using Ohm's law:
$V_{R} = I \cdot R_{i n t e r n a l} = 4.545 A \cdot 1 Ω \approx 4.545 V$
Step 5: Calculate the potential difference across the capacitor
The potential difference $V_{C}$ across the capacitor at steady state is given by the EMF of the battery minus the voltage drop across the internal resistance:
$V_{C} = V_{b a t t e r y} - V_{R} = 50 V - 4.545 V \approx 45.455 V$
Final Answer
The potential difference across the capacitor at steady state is approximately 45.46 V.
---

Updated on:18/9/2024

|

Class 12 PHYSICS ELECTROSTATICS

Similar Questions

Knowledge Check

In the circuit shown, the cell is ideal , with $e m f = 15 V$ . Ecah resistance is of $3 Ω .$ the potential difference across the capacitor is

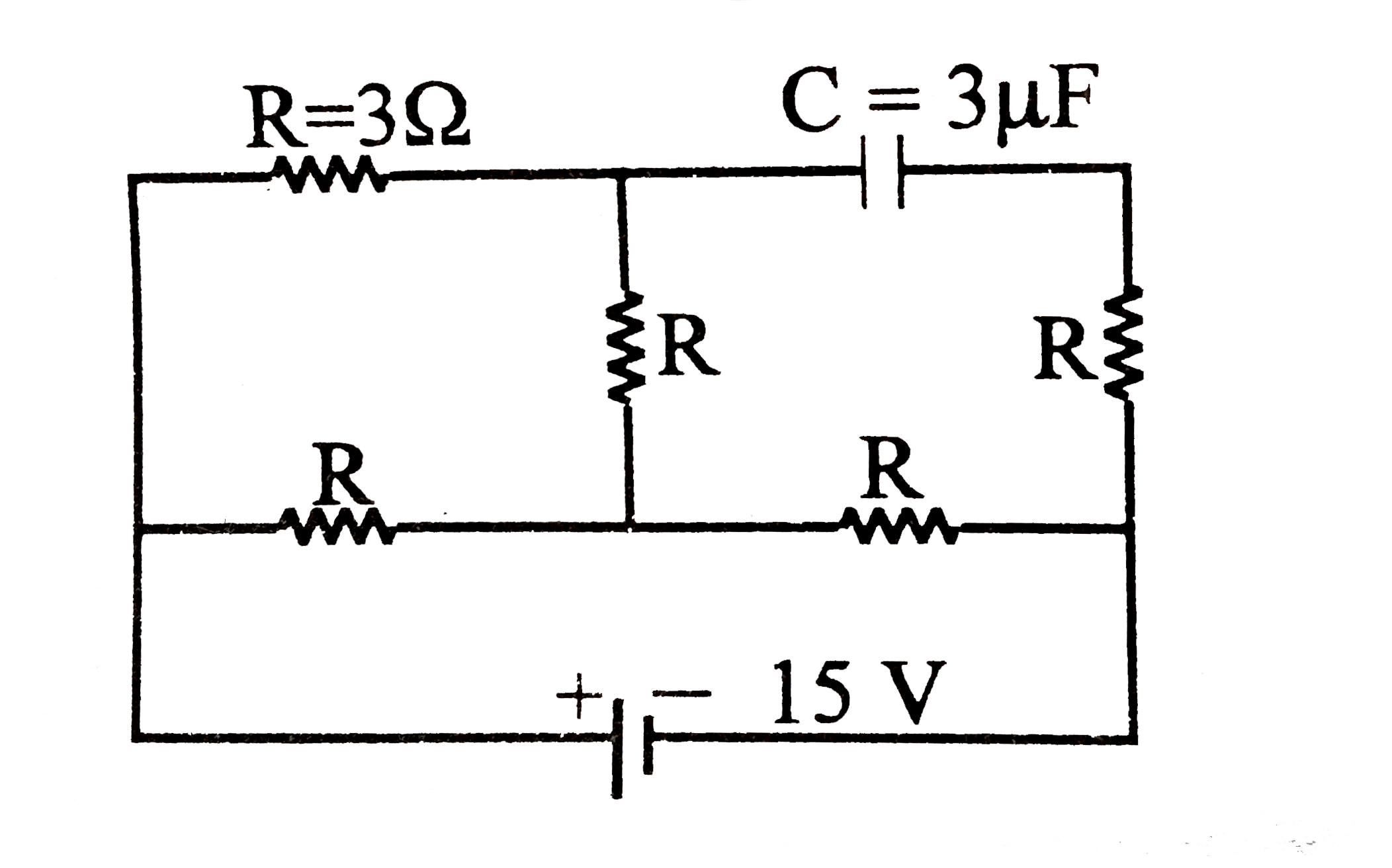Azero
B $9 V$
C $12 V$
D $15 V$
Three resistances $2 Ω, 4 Ω, 5 Ω$ are combined in series and this combination is connected to a battery of 12 V emf and negligible internal resistance. The potential drop across these resistances are
A $(5, 45, 4.36, 2.18) V$
B $(2, 18, 5.45, 4.36) V$
C $(4.36, 2.18, 5.45) V$
D $(2.18, 4.36, 5.45) V$
A voltmeter has a resistance of $50 Ω$ is connected across a cell of e.m.f. 2V and internal resistance $10 Ω$ . The reading of voltmeter is
A1.667V
B16.7V
C167V
D0.167V

Recommended Questions

Home
Ask Doubt
Profile