Two capacitances of capacity C1and C2 are connected in series and potential difference V is applied across it. Then the potential difference across C1 will be
V2
(C22C21+C22)V
(C1C1+C2)V
(C2C1+C2)V
The correct Answer is:D
In series, the charge on both capacitors is equal Let the steady state charge on each capacitor be Q.
Then, Q=CeqV=(C1C2C1+C2)V
So, potential difference across the capacitor of capacitance C1,V1=QC1=(C2C1+C2)V.
Similar Questions
Knowledge Check
Find the potential difference across C2.
 A6 VB4 VCzeroD2 V
A6 VB4 VCzeroD2 VThree capacitors of capacitance 1μF,2μF and 3μF are connected in series and a potential difference of 11V is applied across the combination. Then, the potential difference across the plates of 1μF capacitor is
A2VB4VC1VD6VTwo capacitors 3μF and 6μF are connected in series across a potential difference of 120V. Then the potential difference across 3μF capacitor is:
A40VB60VC80VD100V
Two capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
View SolutionTwo capacitors of 3μF and 6μF are connected in series and a potential difference of 900 V is applied across the combination. They are then disconnected and reconnected in parallel. The potential difference across the combination is
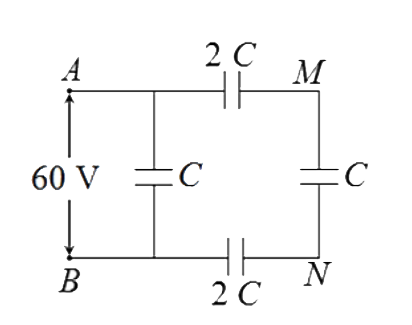
View SolutionIn the circuit shown, a potential difference of 60V is applied across AB. The potential difference between the point M and N is
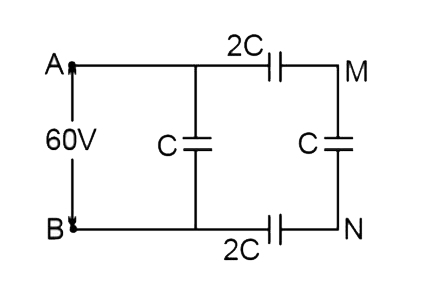
View SolutionTwo capacitors of 1μFand2μF are connected in series and this combination is charged upto a potential difference of 120 volt. What will be the potential difference across 1 micro farad capacitor ?
View SolutionTwo capacitors of capacitances 3μFand5μF respectively are connected in parallel and this combination is connected in series with a third capacitor of capacitance 2μF. A potential difference of 100 V is applied across the entire combination. The charge and the potential difference across the third capacitor is
View Solution