A uniform cylindrical rod of length L and radius r, is made from a material whose Young’s modulus of elasticity equals Y. When this rod is heated by temperature T and simultaneously subjected to a net longitudinal compressional force F, its length remains unchanged. The coefficient of volume expansion, of the material of the rod, is (nearly) equal to:
3F/(πr2YT)
6F/(πr2YT)
F/(3πr2YT)
9F/(πr2YT)
The correct Answer is:A
To solve the problem, we need to analyze the situation where a cylindrical rod is subjected to both thermal expansion due to heating and a compressive force. The key is to understand how these two factors interact when the length of the rod remains unchanged.
1. Understand the Effects of Heating:
When the rod is heated, it tends to expand. The change in length (ΔL) due to thermal expansion can be expressed using the formula:
ΔL=L⋅α⋅T
where α is the coefficient of linear expansion and T is the change in temperature.
2. Understand the Effects of Compression:
The compressive force F applied to the rod will cause a change in length as well, which can be expressed using Hooke's Law:
ΔL=−FLAY
where A is the cross-sectional area of the rod, Y is Young's modulus, and L is the original length of the rod.
3. Set the Changes in Length Equal:
Since the length of the rod remains unchanged, the expansion due to heating must be equal to the contraction due to the compressive force:
L⋅α⋅T=FLAY
4. Simplify the Equation:
We can cancel L from both sides (assuming L≠0):
α⋅T=FAY
5. Express the Coefficient of Volume Expansion:
The coefficient of volume expansion β is related to the coefficient of linear expansion α by the relationship:
β=3α
Therefore, we can express α in terms of β:
α=β3
6. Substitute for Alpha:
Substitute α back into the equation:
β3⋅T=FAY
7. Solve for Beta:
Rearranging gives:
β=3FAYT
Final Expression:
The coefficient of volume expansion β of the material of the rod is given by:
β=3FAYT
When the rod is heated, it tends to expand. The change in length (ΔL) due to thermal expansion can be expressed using the formula:
ΔL=L⋅α⋅T
where α is the coefficient of linear expansion and T is the change in temperature.
The compressive force F applied to the rod will cause a change in length as well, which can be expressed using Hooke's Law:
ΔL=−FLAY
where A is the cross-sectional area of the rod, Y is Young's modulus, and L is the original length of the rod.
Since the length of the rod remains unchanged, the expansion due to heating must be equal to the contraction due to the compressive force:
L⋅α⋅T=FLAY
We can cancel L from both sides (assuming L≠0):
α⋅T=FAY
The coefficient of volume expansion β is related to the coefficient of linear expansion α by the relationship:
β=3α
Therefore, we can express α in terms of β:
α=β3
Substitute α back into the equation:
β3⋅T=FAY
Rearranging gives:
β=3FAYT
The coefficient of volume expansion β of the material of the rod is given by:
β=3FAYT
Similar Questions
A steel cylindrical rod of length l and radius r is suspended by its end from the ceiling.
(a) Find the elastic deformation energy U of the rod.
(b) Define U in terms of tensile strain Δl/l of the rod.
View SolutionA thin uniform rod of mass M and length l is rotating about a frictionless axis passing through one of its ends and perpendicular to the rod. The rod is heated uniformly to increases its temperature by Δθ. Calculate the percentage change in rotational kinetic energy of the rod. Explain why the answer is not zero. Take coefficient of linear expansion of the material of the rod to be α.
View Solution
Knowledge Check
A cylinder of length l and radius r is heated to temperature T. A longitudeinal compressive force F is applied on cylinder to keep its length same. Find coefficient of volume expansion.
AFYtπr2B3FYtπr2C2FYtπr2DNone of theseA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y, then the work done is proportional to
AYB1/YCY2D1/Y2A metallic rod of length l and cross - sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y, then the work done is proportional to
AyB1yCy2D1y2
A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA metallic rod of length 'L' and cross-section 'A' has Young's modulus 'Y' and coefficent of linear expansion 'α'. If the rod is heated to a temperature. 'T' the energy stored per unit volume is:
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
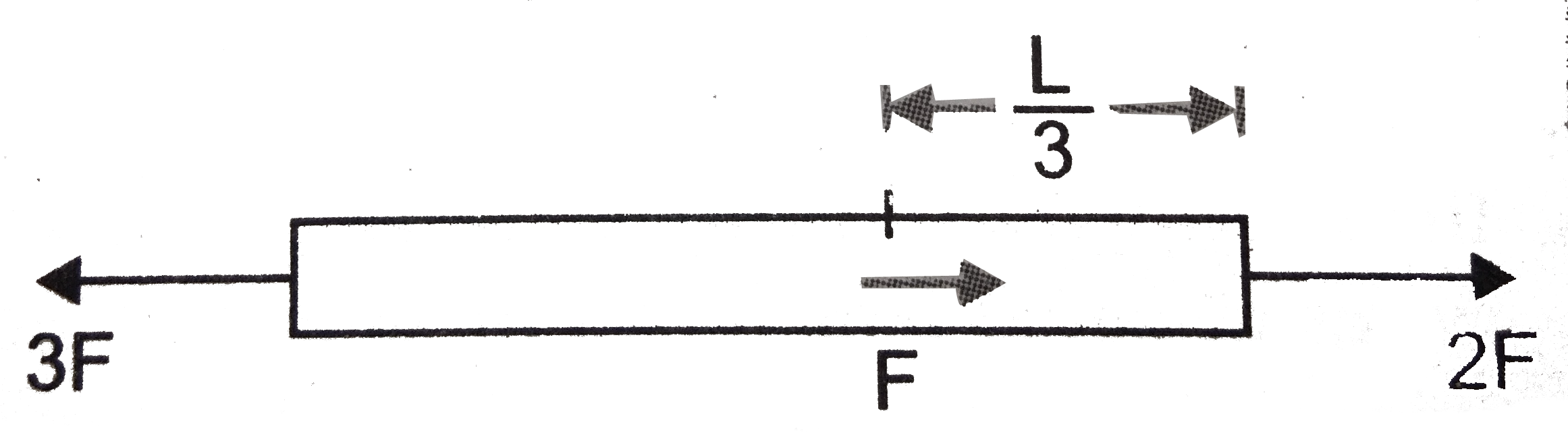
View SolutionA uniform metal rod of length L and mass M is rotating about an axis passing throuth one of the ends perpendicular to the rod with angular speed ω. If the temperature increases by t∘C then the change in its angular velocity is proportional to which of the following ? (Coefficient of linear expansion of rod =α)
View SolutionTwo ends of rods of length L and radius R of the same material of kept at the same temperature. Which of the following rods conducts the maximum heat?
View Solution
