
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
0.36 kg
1.2 kg
2.4 kg
3.6 kg
The correct Answer is:C
Sample of ice has been receiving heat at constant rate P from water. Its temperature has increased by 30°C in time 60 min.
Therefore misiΔTiP=60min⇒m=(60×60s)×(42W)(2100J/kg).(30∘C)=2.4kg
misiΔTiP=60min⇒m=(60×60s)×(42W)(2100J/kg).(30∘C)=2.4kg
Similar Questions
Find the quantity of heat required to convert 40 g of ice at −20∘C into water at 20∘C. Given Lice=0.336×106Jkg. Specific heat of ice = 2100 J/kg-K
Specific heat of water = 4200 J/kg-K
View SolutionAn ice block of volume 3.2×10−5m3 and at temperature 0∘C is put in 200 gm water at 10∘C. Find the temperature and composition of mixture when thermal equilibrium is attained. Given that density of ice is 900kg/m3, specific heat of water is 4200J/kg∘ C and latent heat of fusion of ice .4×10−5J/kg
View Solution
Knowledge Check
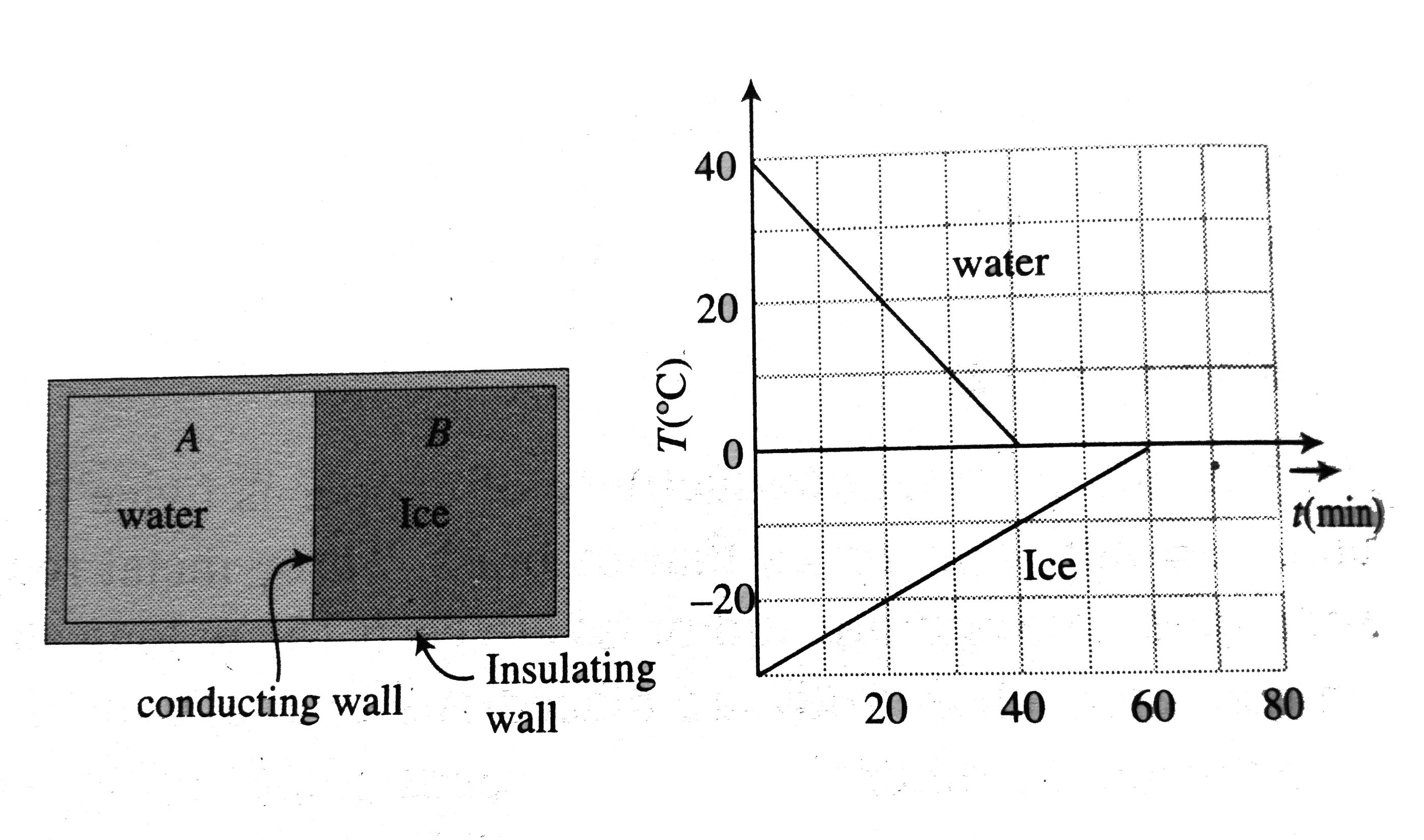
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal toA0.12 kgB0.15 kgC0.25 kgD0.40 kgA metal piece weighing 15g is heated to 100∘C and then immersed in a mixture of ice and water at the thermal equilibrium. The volume of the mixture is found to be reduced by 0.15cm3 with the temperature of mixture remaining constant. Find the specific heat of the metal. Given specific gravity of ice =0.92, specific gravity of water at 0∘C=1.0, latent heat of fusion of ice =80cal−g−1.
A0.092cal/gm∘CB0.124cal/gm∘CC0.162cal/gm∘CD0.242cal/gm∘CThe temperature in which ice, water and water vapour exist in equilibrium is called
AFreezing point,BBoiling point,CCritical point,DTriple point.
A piece of ice of mass 40 g is dropped into 200 g of water at 50∘C. Calculate the final temperature of water after all the ice has melted (sp. heat capacity of water =4200J/kg∘C, sp. latent heat of fusion of ice = 336×103J/kg)
View SolutionAt 0∘C a thermally isolated container has 200 g of water. When air above water is pumped out, then some of water evaporates and some of it freezes. What will be the mass of ice formed on freezing when there will be no water left in container? Latent heat of vaporisation of water = 2.2×106 J/kg and latent heat of fusion of ice = 3.37×105 J/kg.
View Solution(a) Two 40g ice cubes are droped into 200g of water in a thermally insulated container. If the water is initially at 25∘C, and the ice comes directly from a freezer at −15∘C, what is the final temperature at thermal equilibrium? (b) What is the final temperature if only one ice cube is used ?
View SolutionIn an insulated vessel, 250 g of ice at 0∘C is added to 600 g of water at 18∘C
(a) What is the final temperature of the system?
(b) How much ice remains when the system reaches equilibrium?
Useful data:
Specific heat capacity of water: 4190 K/K.kg
Speicific heat capacity of ice: 2100J/K.kg
Latent heat of fusio of ice: 3.34×105J/kg
View SolutionWater at 10∘C is present in a thermally insulated container. Calculate the ratio of mass of ice formed and initial mass of water, if a small crystal of ice is thrown into it.
View Solution
