Question

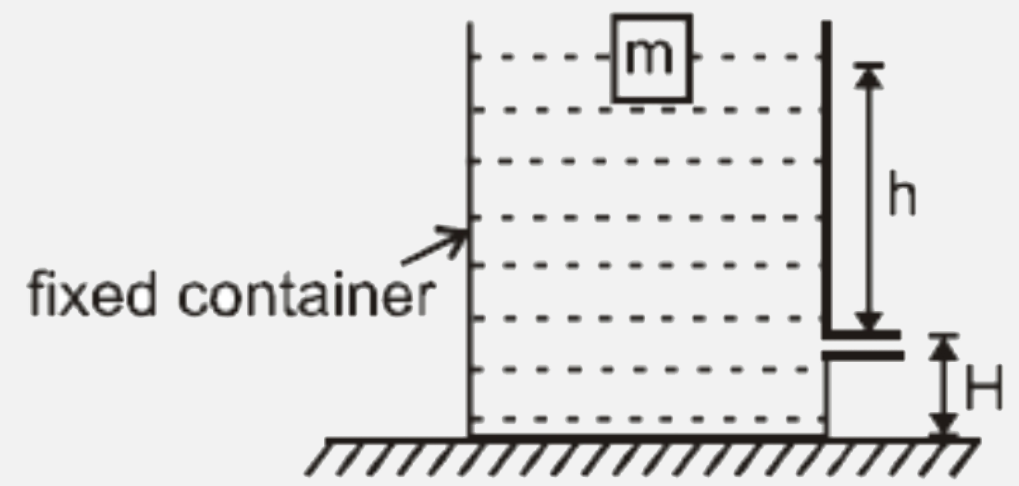
A solid sphere of radius $R$ made of a material of bulk modulus $B$ is surrounded by a liquid in a cylindrical container. A massless piston of area $A$ (the area of container is also $A$) floats on the surface of the liquid. When a mass $M$ is placed on the piston to compress the liquid , fractional change in radius of the sphere is $\frac{Mg}{\alpha AB}$. Find the value of $\alpha$.

Answer

9

Explanation

Increase in pressure is `Deltap=(Mg)/(A)`
Bulk modulus is `B=(DeltaP)/((DeltaV//V))`
`therefore(DeltaV)/(V)=(DeltaP)/(B)=(Mg)/(AB)` … (i)
Also, the volume of the sphere is
`V=(4)/(3)piR^(3)rArr(DeltaV)/(V)=(3DeltaR)/(R)or(DeltaR)/(R)=(1)/(3).(DeltaV)/(V)`, using eq . (i) we get
`(DeltaR)/(R)=(Mg)/(3AB)thereforen=9`