‘cold box’ in the shape of a cube of edge 50 cm is made of ‘thermocol’ material 4.0 cm thick. If the outside temperature is 30∘C the quantity of ice that will melt each hour inside the ‘cold box’ is : (the thermal conductivity of the thermocol material is 0.050 W/mK)
1.52 kg
0.605 kg
2.520 kg
0.512 kg
The correct Answer is:B
To solve the problem of how much ice will melt in the cold box made of thermocol, we will follow these steps:
Step 1: Understand the Problem
We have a cold box in the shape of a cube with:
- Edge length = 50 cm
- Thickness of thermocol = 4 cm
- Outside temperature = 30°C
- Thermal conductivity of thermocol (K) = 0.050 W/mK
- Latent heat of fusion of ice (L) = 80 cal/g = 334,000 J/kg (after conversion)
Step 2: Convert Units
Convert the dimensions from centimeters to meters:
- Edge length of the cube = 50 cm = 0.5 m
- Thickness of thermocol = 4 cm = 0.04 m
Step 3: Calculate the Area
The total surface area (A) of the cube can be calculated as:
A=6×(side length)2
A=6×(0.5m)2=6×0.25=1.5m2
Step 4: Determine the Temperature Difference
The temperature difference (ΔT) between the inside and outside of the box is:
ΔT=Toutside−Tinside=30°C−0°C=30K
Step 5: Calculate the Heat Transfer
Using Fourier's law of heat conduction, the heat transfer (Q) through the thermocol in one hour can be calculated as:
Q=K⋅A⋅ΔTΔx⋅t
Where:
- K=0.050W/mK
- A=1.5m2
- ΔT=30K
- Δx=0.04m
- t=3600s (1 hour)
Substituting the values:
Q=0.050⋅1.5⋅300.04⋅3600
Step 6: Calculate Q
Calculating the first part:
Q=0.050⋅1.5⋅300.04=2.250.04=56.25W
Now, multiplying by time:
Q=56.25⋅3600=202500J
Step 7: Relate Heat to Mass of Ice
The heat required to melt mass m of ice is given by:
Q=m⋅L
Where L=334,000J/kg (latent heat of fusion of ice).
Step 8: Solve for Mass (m)
Rearranging the equation gives:
m=QL=202500334000
Step 9: Calculate m
Calculating the mass:
m≈0.605kg
Final Answer
The quantity of ice that will melt each hour inside the cold box is approximately 0.605 kg.
We have a cold box in the shape of a cube with:
- Edge length = 50 cm
- Thickness of thermocol = 4 cm
- Outside temperature = 30°C
- Thermal conductivity of thermocol (K) = 0.050 W/mK
- Latent heat of fusion of ice (L) = 80 cal/g = 334,000 J/kg (after conversion)
Convert the dimensions from centimeters to meters:
- Edge length of the cube = 50 cm = 0.5 m
- Thickness of thermocol = 4 cm = 0.04 m
The total surface area (A) of the cube can be calculated as:
A=6×(side length)2
A=6×(0.5m)2=6×0.25=1.5m2
The temperature difference (ΔT) between the inside and outside of the box is:
ΔT=Toutside−Tinside=30°C−0°C=30K
Using Fourier's law of heat conduction, the heat transfer (Q) through the thermocol in one hour can be calculated as:
Q=K⋅A⋅ΔTΔx⋅t
Where:
- K=0.050W/mK
- A=1.5m2
- ΔT=30K
- Δx=0.04m
- t=3600s (1 hour)
Q=0.050⋅1.5⋅300.04⋅3600
Calculating the first part:
Q=0.050⋅1.5⋅300.04=2.250.04=56.25W
Now, multiplying by time:
Q=56.25⋅3600=202500J
The heat required to melt mass m of ice is given by:
Q=m⋅L
Where L=334,000J/kg (latent heat of fusion of ice).
Rearranging the equation gives:
m=QL=202500334000
Calculating the mass:
m≈0.605kg
The quantity of ice that will melt each hour inside the cold box is approximately 0.605 kg.
Similar Questions
(a) Calculate the rate at which body heat is conducted through the clothing of a skier in a steady-state process, given the following data: the body surface area is 1.8m2, and the clothing is 1.0 cm thick , the skin surface temperature is 33∘C and the outer surface of the clothing is at 1.0∘C, the thermal conductivity of the clothing is 0.040W/m.K. (b) If , after a fall, the skier's clothes became soaked with water of thermal conductivity 0.60W/m.K, by how much is the rate of conduction multiplied ?
View SolutionA 100 W heater is placed in a cubical container of edge length 6×10−2m. The wall thick ness of the container is 1 mm. If inside and outside temperature in steady state are 30∘C. and 25∘C, find the thermal conductivity of the material of the box.
View Solution
Knowledge Check
5cm thick walls of a box like cooler is made of plastic toam. Its total surface area is 1.5m2. If outside temperature is 30∘C, then how much ice melts each hour inside the cooler to old its temperature at 0∘C.
(Given K for plastic =0.04W/mK,L0=80cal/g and 1kcal=4.184kJ/kcal)A4kgB0.39kgC3.9kgD0.2kgOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
A3×103JB6×103JC9×103JD12×103J1.56×105J of heat is conducted through is 2m2 wall of 12 cm thick in one hour. Temperature difference between the two sides of the wall is 20∘C. The thermal conductivity of the material of the wall is (in Wm−1K−1)
A0.11B0.13C0.15D1.2
A cubical thermocol ice box of side length 30cm has thichess of 5.0cm If 4.0kg of ice is put in the box estimate the amount of ice remaining after 6hr The utside temperature is 45∘C and co-efficinet of the thermal conductivity of the thermocol is 0.01Js−1m−1K1 (Latent Heat of fusion of water =335×103Jkg−1) .
View SolutionA thermocole cubical icebox of side 30 cm has a thickness of 5.0 cm if 4.0 kg of ice are put ini the box, estimate the amount of ice remaining after 6 h. The outside temperature is 45∘C and coefficient of thermal conductivity of thermocole=0.01J/kg.
View SolutionA cubical ice box of side 50 cm has a thickness of 5.0 cm. if 5 kg of ice is put in the box, estimate the amount of ice remaining after 4 hours. The outside temperature is 40∘C and coefficient of thermal conductivity of the material of the box = 0.01Js−1m−1.∘C−1. Heat of fusion of ice=335Jg−1.
View SolutionA electric heater is placed inside a room of total wall area 137m2 and maintained at a temperature 20∘C inside, outside temperature −10∘C. The walls are made up of three composite materials. The innermost layer is made up of wood of thickness 2.5 cm, the middle layer is of cement of thickness 1 cm and the exterior layer is 25 cm thick. Assuming there is no loss of heat through any other way, the power of the electric heater is (the thermal conductivity of wood, cement and brick are 0.125 W m2∘C−1,1.5Wm−2∘C−1and1Wm−2∘C−1 respectively)
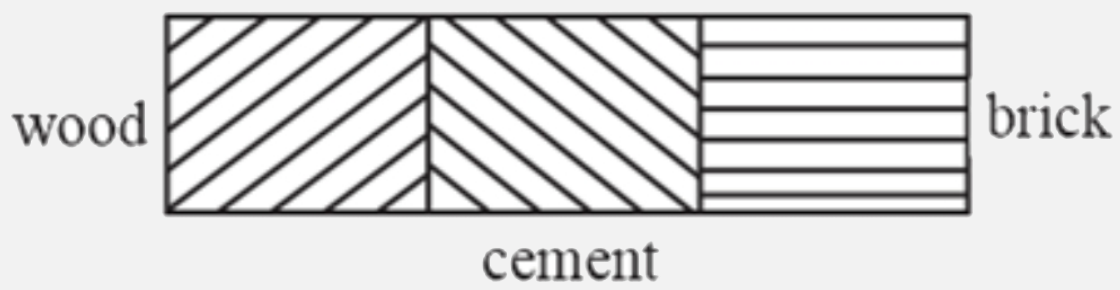
View SolutionA closed cubical box made of a perfectly insulating material has walls of thickness 8 cm and the only way for the heat to enter or leave the box is through two solid cylinderical metal plugs , each of cross - sectional area 12cm2 and length 8 cm fixed in the opposite walls of the box . The outer surface A of one plug is kept at a temperature of 100∘C while the outer surface of the other plug is maintained at a temperature of 4∘C~.Thethermalco∈ductivityofthematerialoftheplugis0.5 cal // cmsec""^(@)C.Asourceofe≠rgy≥≠rat∈g36 cal s^(-1) is enclosed inside the box . Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface
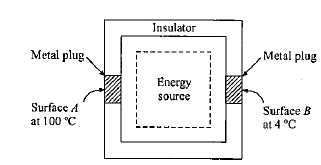
View Solution
