State Hooke's law.
Step-by-Step Solution:
1. Definition of Hooke's Law: Hooke's Law states that the strain produced in a solid material is directly proportional to the applied stress, provided the material is within its elastic limit.
2. Understanding Stress and Strain:
- Stress: It is defined as the force (F) applied per unit area (A) of the material. Mathematically, it can be expressed as:
Stress=FA
- Strain: It is the measure of deformation representing the displacement between particles in a material body. It is defined as the change in length (ΔL) divided by the original length (L):
Strain=ΔLL
3. Proportionality Statement: According to Hooke's Law, the relationship can be expressed as:
Stress∝Strain
This can also be written as:
Stress=k×Strain
where k is the proportionality constant known as the modulus of elasticity.
4. Elastic Limit: Hooke's Law is valid only up to a certain limit known as the elastic limit. Within this limit, when the applied stress is removed, the material will return to its original shape. Beyond this limit, the material may undergo permanent deformation.
5. Conclusion: Therefore, Hooke's Law can be summarized as:
- The strain produced in a solid is directly proportional to the applied stress, as long as the material is within its elastic limit.
---
- Stress: It is defined as the force (F) applied per unit area (A) of the material. Mathematically, it can be expressed as:
Stress=FA
- Strain: It is the measure of deformation representing the displacement between particles in a material body. It is defined as the change in length (ΔL) divided by the original length (L):
Strain=ΔLL
Stress∝Strain
This can also be written as:
Stress=k×Strain
where k is the proportionality constant known as the modulus of elasticity.
- The strain produced in a solid is directly proportional to the applied stress, as long as the material is within its elastic limit.
Similar Questions
Knowledge Check
A mass M attached to a spring oscillates with a period of 1s. If the mass is increased by 3 kg the period increases by 1s. What is the value of M, assuming that Hooke's law is obeyed ?
A3 kgB2 kgC1 kgD5 kgThe graph show the behaviour of a length of wire in the region for which the substances obeys Hooke's law. P and Q represent
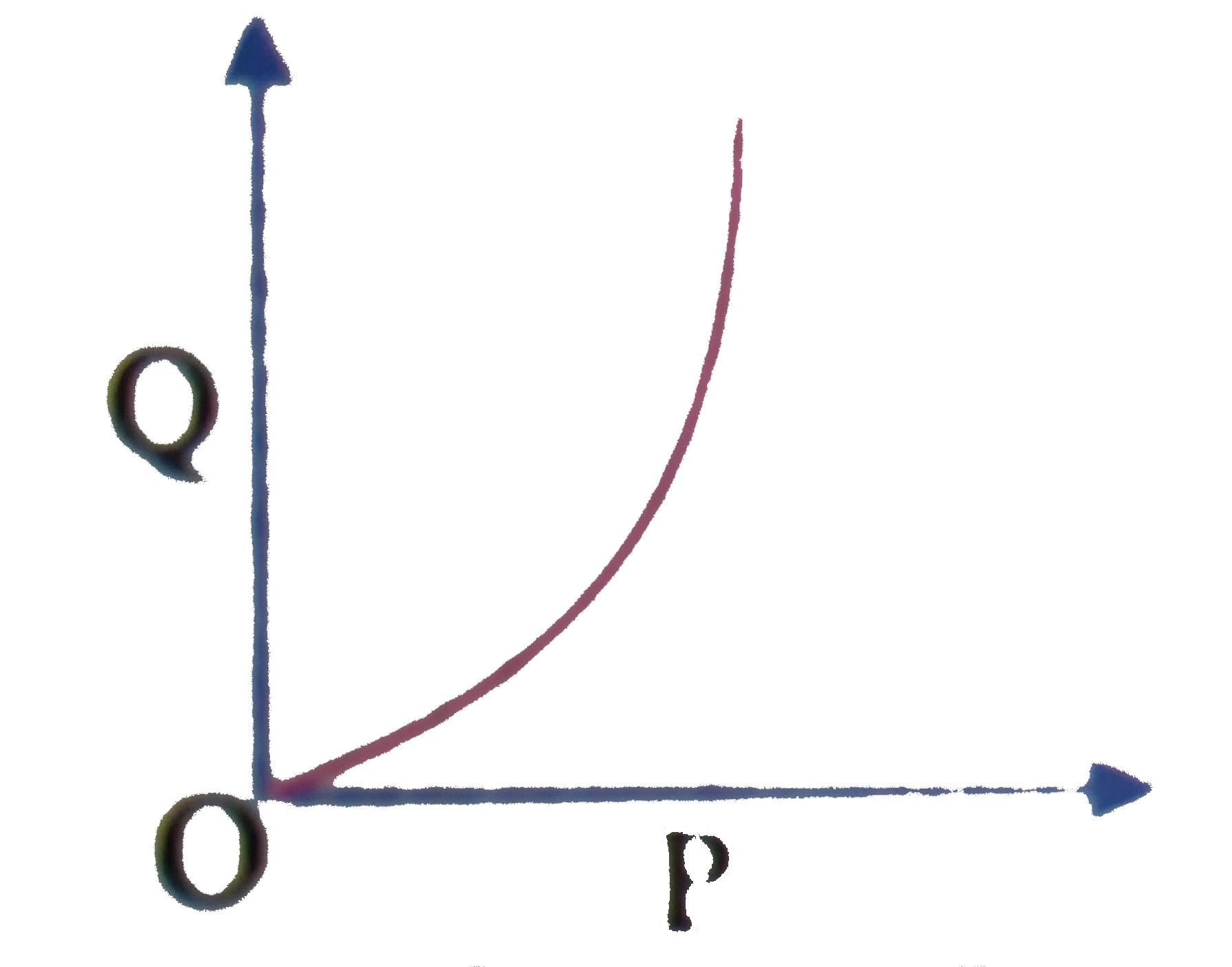 AP = applied force, Q = extensionBextension, applied forceCextension, stored elastic energyDstored elastic energy, extension
AP = applied force, Q = extensionBextension, applied forceCextension, stored elastic energyDstored elastic energy, extension
A mass m attached to a spring oscillates with a period 2s. If the mass is increased by 2kg, the period increases by 1s. Find the initial mass m, asssuming that Hooke's law is obeyed.
View SolutionA mass M attached to a spring oscillates with a period of 2s. If the mass is increased by 2 kg, then the period increases by 2s. Find the initial mass M assuming that Hooke's law is obeyed.
View SolutionA mass M, attached to a spring, oscillates with a period of 2s. If the mass is increased by 4kg, the time period increases by one second. Assuming that Hooke's law is obeyed, find the initial mass M.
View SolutionState and prove Hooke's law.
View SolutionDefine stress and strain and derive their units. What is Hooke's law? Write its one limitation.
View SolutionDraw the variation of potential energy and kinetic energy of a block attached to a spring, which obeys Hooke's law.
View Solution
