A point tube is mounted on an aeroplane wing to measure the speed of the plane. The tube contains alcohol and shows a level difference of 40 cm. What is the speed of the plane reative to air ? (sp. Gr. Of alcohol = 0.8 and density of air = 1 kg m−3).
A Pitot tube (also called Prandt tube or Wind speed indicator) consists of a bent tube ABCD with small apertures at A and D. This tube is inserted in pipe P through which the fluid (air in this case) is flowing. Let ρ be the density of air. The plane of the aperture A is parallel to the direction of air flow. As such, the velocity (v1) of air at A is the same as its velocity in pipe (which is equal to the velocity v of plane relative to air). Let P1 be the pressure at A. The plane of the aperture at D is normal to the direction of air-flow in the pipe. The velocity (v2) of air-flow rapidly falls to zero at D and the pressure increases to P2 . Applying Bernoulli’s theorem to the horizontal flow at A and D, we get
P1+12ρv21=P2+12ρv22orv=√2(P1−P2)ρ) (as v1=v and v2=0 )
but P1−P2=hσg where σ is the density of the liquid in the tube ABCD.
As h=40cm=0.4m,σ=0.8×1000kg/m3,ρ=1kg/m3,v=√2×0.4(0.8×1000)9.81m/s=79.2m/s
Similar Questions
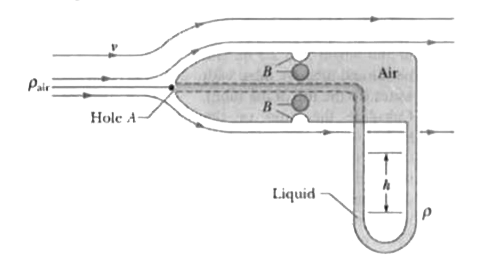
A pitot tube Fig. is used to determine the air speed of an airplane. It consists of an outer tube with a number of small holes B (four are shown that allow air into the tube, that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes stagnant so that vA = 0. At B, however, the speed of the air presumably equals the airspeed v of the plane. (a) Use Bernoulli's equation to show that
v=√2ρghρair
where ρ is the density of the liquid in the U-tube and his the difference in the liquid levels in that tube. (b) Suppose that the tube contains alcohol and the level difference h is 20.0 cm. What is the plane's speed relative to the air? The density of the air is 1.03kg/m3 and that of alcohol is 810 kg/m3
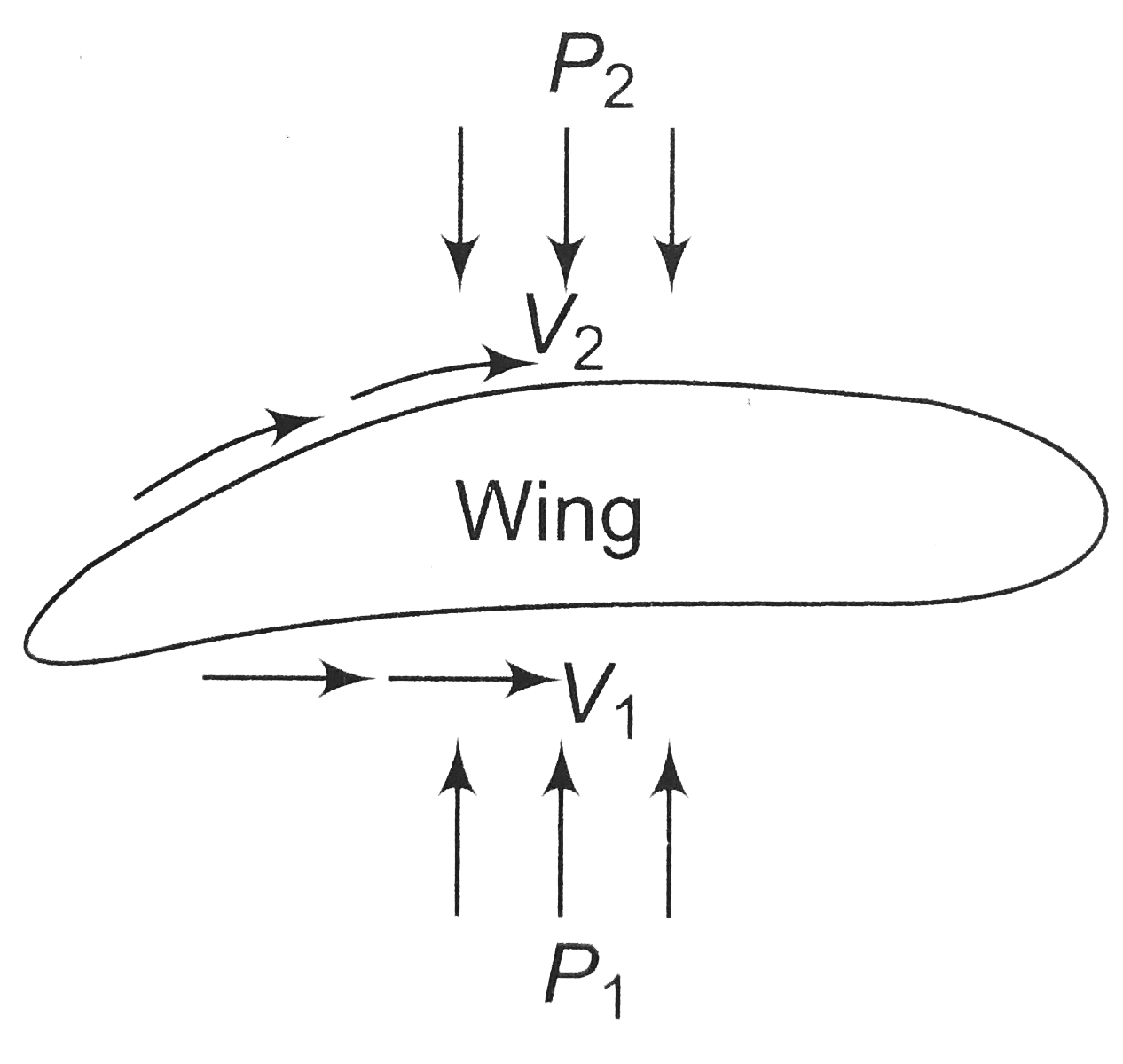
View SolutionIn a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surface of the wing are 70ms−1and63ms−1 respectivley. What is the lift on the wing if its area is 2.5m2? Take the density of air is 1.3kgm−3.
View Solution
Knowledge Check
The speed of flow past the lower surface of a wing of an aeroplane is 50ms−1. What speed of flow over the upper surface will give a dynamic lift of 1000Pa? Density of air =1.3kgm−3
 A25.55m/sB63.55m/sC13.25m/sDNone of these
A25.55m/sB63.55m/sC13.25m/sDNone of theseIn a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70ms−1 and 83ms−1 respectively. What is the lift on the wing, if its area is 2.5m2? Take the density of air to be 1.3kgm−3
A1513NB1513 dinesC151.3 ND151.3 dynesA plane is in level flight at constant speed and each of the two wings has an area of 25m2. If the speed of the air on the upper and lower surfaces of the wing are 270kmh−1 and 234kmh−1 respectively, then the mass of the plane is (take the density of the air = 1kgm−3)
A1550 kgB1750 kgC3500 kgD3200 kg
An aeronautical engineer observed that on the upper and the lower surface of the wing of an aeroplane the speed of the air are 120ms−1and90ms−1 respectively during flight. What is the lift on the wing of aeroplane if its area is 3.2m2? Given density of air is 1.29kg/m3.
View SolutionEach of the two wings of an aeroplane has area 30m2. The speed of the air on the upper and lower surfaces of theon the wing of aeroplane are 90ms−1 and 70ms−1 respectively. If the plane is in level flight at constant speed, find the uplift and the mass of the aeroplane. Given density of air =1.29kgm−3.
View SolutionA fully loaded Boeing aircraft has a mass of 3.3×105kg. Its total wing area is 500m2 . It is in level flight with a speed of 960km/h.
(a) Estimate the pressure difference between the lower and upper surfaces of the wings
(b) Estimate the fracitional increases in the speed of the air on the upper surfaces of the wing relative to the lower surface. The density of air is 1.2kg/m3.
View SolutionA plane is in level flight at constant speed and each of its two wings has an area of 25m2 . If the speed of the air on the upper and lower surfaces of the wing are 270kmh−1 and 234kmh−1 respectively, then the mass of the plane is (Take the density of the air =1kgm−3)
View SolutionAir stream flows horizontally past an aeroplane wing of surface area 4m2. The speed of air over the top surface is 60ms−1 and under the bottom surface is 40ms−1 The force of lift on the wing is (density of air =1kgm−3)
View Solution
