A particle is suspended vertically from a point O by an inextensible mass less string of length L. A vertical line AB is at a distance of L8 from O as shown in figure. The particle is given a horizontal velocity u. At some point, its motion ceases to be circular and eventually the object passes through the line AB. At the instant of crossing AB, its velocity is horizontal. Find u.

The correct Answer is:4
It is clear from the statement of the problem that the particle leaves the circular path before it crosses the line AB second time, during its upward motion.
Let us assume that the particle leaves the circular path at ‘P’ and v is the velocity of the particle at P. Then, conservation of mechanical energy at P and at the lowest point yields :
12mu2=12mv2+mgL(1+sinθ) ....(i)
At point P:T=mgsinθ=mv2L. If T becomes zero. v2=gLsinθ .....(ii)
After leaving the circular path, the particle moves along a parabolic trajectory as a projectile.
As it is given that velocity of the particle when it crosses AB is horizontal, it is clear that, when it is crossing AB, it is passing through its highest point in the parabolic path.
⇒12×Range=Lcosθ−L8
v2sin2(90−θ)2g=Lcosθ−L8 ....(iii)
From (ii) and (iii), cosθ=12⇒θ=60∘
Using this in (i) , we get
u=
⎷[4+3√32gL]

Similar Questions
Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
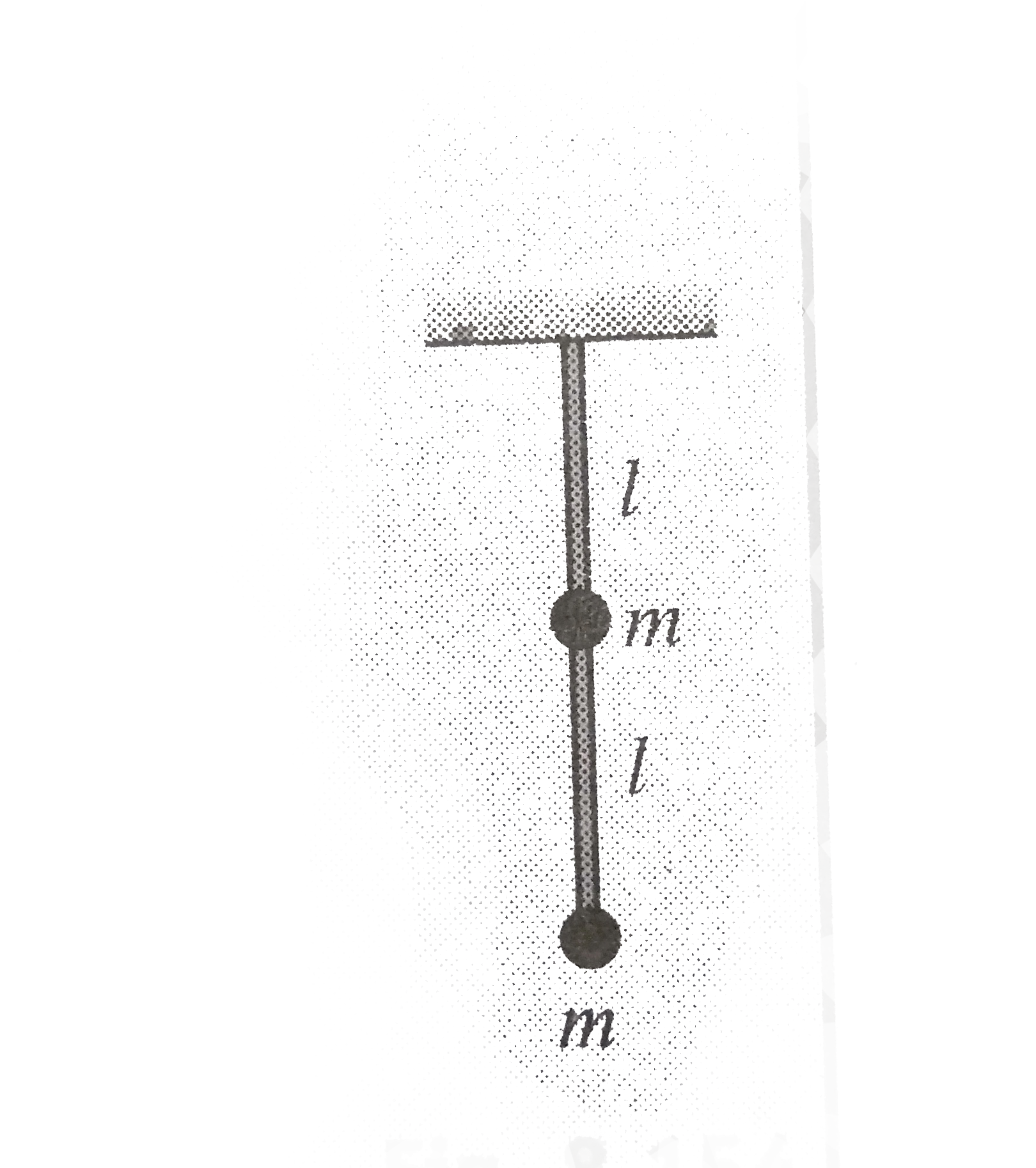
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View Solution
Knowledge Check
As shown in figure, a particle of mass m is performing vertical circular motion. The velocity of the particle is increased, then at which point will the string break?
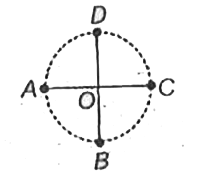 AABBCCDD
AABBCCDDA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass m is suspended from point O and undergoes circular motion in horizontal plane as conical pendulum as shown in figure.
 AAngular momentum of particle about point of suspension does not remains constant.BAngular momentum of particle about centre of circle remains constant.CAverage force during half rotation is 2mgtanthethaπDAverage torque about axis OC during half rotation is zero
AAngular momentum of particle about point of suspension does not remains constant.BAngular momentum of particle about centre of circle remains constant.CAverage force during half rotation is 2mgtanthethaπDAverage torque about axis OC during half rotation is zero
A particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View SolutionA particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
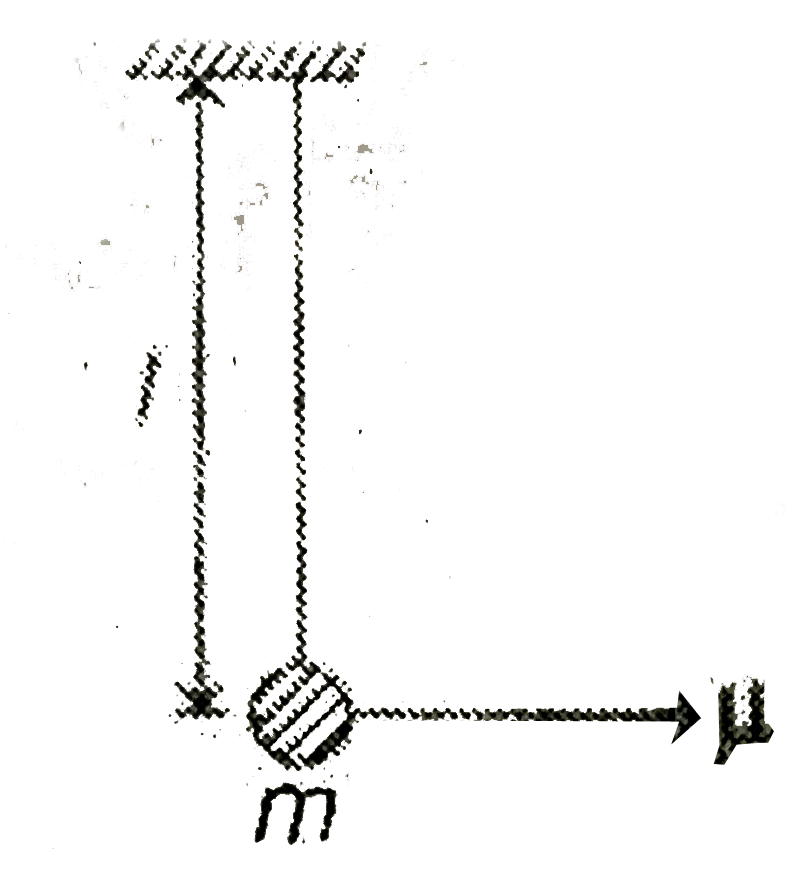
The tension in the string at an instant when acceleration of the particle is horizontal and √3g is
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
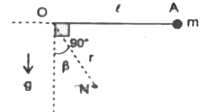
View Solution
