A small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure. When the distance of the piston from closed end is L=L0 the particle speed is v=v0 The piston is moved inward at a very low speed V such that V<<dLLv0, where dL is the infinitesimal displacement of the piston. Which of the following statements(s) is(are) correct?
After each collision with the piston, the particle speed increases by 2V
If the piston moves inward by dL, the particle speed increases by 2vdLL
The rate at which the particle strikes the piston is v/L
The particle’s kinetic energy increases by a factor of 4 when the piston is moved inward from L0to12L0
The correct Answer is:A, D
To solve the problem, we need to analyze the motion of the particle inside the tube and how it interacts with the moving piston. Let's break it down step by step.
Step 1: Understand the Initial Conditions
- The particle of mass m is moving inside a hollow tube.
- The tube is closed at one end and has a movable piston at the other end.
- Initially, when the distance of the piston from the closed end is L=L0, the speed of the particle is v=v0.
Step 2: Analyze the Motion and Collisions
- The particle undergoes elastic collisions with the piston and the closed end of the tube.
- When the particle collides elastically with the piston, its speed will change based on the conservation of momentum and kinetic energy.
- After colliding with the piston, the speed of the particle will increase.
Step 3: Determine the Speed After Collision
- The speed of the particle after the first collision with the piston can be calculated. Since it is an elastic collision, the speed of the particle after the collision becomes:
v′=2v0
This is because the piston is heavy and does not move significantly compared to the particle.
Step 4: Calculate the Time Taken for Piston Movement
- The piston moves inward at a very low speed V such that V≪dLLv0.
- If the piston moves by an infinitesimal distance dL, the time taken for this movement is:
T=dLV
Step 5: Calculate the Number of Collisions
- The particle travels a total length of 2L (to the closed end and back) in time T.
- The number of collisions in time T can be calculated as:
Number of Collisions=v02L⋅T=v02L⋅dLV
Step 6: Increment in Velocity After Collisions
- The increment in velocity after n collisions can be expressed as:
Δv=v0⋅dLL
Thus, the new speed of the particle becomes:
vf=v0+Δv=v0+v0⋅dLL
Step 7: Relate Velocity to Kinetic Energy
- The kinetic energy of the particle is given by:
KE=12mv2
- If the speed doubles, the kinetic energy increases by a factor of 4:
KEf=12m(2v0)2=4⋅12mv20
Conclusion
- After analyzing the situation, we conclude:
1. After each collision with the piston, the particle speed increases by a factor of 2.
2. The kinetic energy increases by a factor of 4 when the piston is moved inward from L0 to L0/2.
Final Statements
- The correct statements are:
- After each collision with the piston, the particle speed increases by a factor of 2.
- The particle's kinetic energy increases by a factor of 4 when the piston is moved inward from L0 to L0/2.
- The particle of mass m is moving inside a hollow tube.
- The tube is closed at one end and has a movable piston at the other end.
- Initially, when the distance of the piston from the closed end is L=L0, the speed of the particle is v=v0.
- The particle undergoes elastic collisions with the piston and the closed end of the tube.
- When the particle collides elastically with the piston, its speed will change based on the conservation of momentum and kinetic energy.
- After colliding with the piston, the speed of the particle will increase.
- The speed of the particle after the first collision with the piston can be calculated. Since it is an elastic collision, the speed of the particle after the collision becomes:
v′=2v0
This is because the piston is heavy and does not move significantly compared to the particle.
- The piston moves inward at a very low speed V such that V≪dLLv0.
- If the piston moves by an infinitesimal distance dL, the time taken for this movement is:
T=dLV
- The particle travels a total length of 2L (to the closed end and back) in time T.
- The number of collisions in time T can be calculated as:
Number of Collisions=v02L⋅T=v02L⋅dLV
- The increment in velocity after n collisions can be expressed as:
Δv=v0⋅dLL
Thus, the new speed of the particle becomes:
vf=v0+Δv=v0+v0⋅dLL
- The kinetic energy of the particle is given by:
KE=12mv2
- If the speed doubles, the kinetic energy increases by a factor of 4:
KEf=12m(2v0)2=4⋅12mv20
- After analyzing the situation, we conclude:
1. After each collision with the piston, the particle speed increases by a factor of 2.
2. The kinetic energy increases by a factor of 4 when the piston is moved inward from L0 to L0/2.
- The correct statements are:
- After each collision with the piston, the particle speed increases by a factor of 2.
- The particle's kinetic energy increases by a factor of 4 when the piston is moved inward from L0 to L0/2.
Similar Questions
A L Shaped tube containing liquid of density pis accelerated horizontally with acceleration as shown in the figure. The end of tube B is closed while end A is open. If the atmospheric pressure is Po. Then the pressure at B is :
View SolutionA20 cm long cylindrical test tube is inverted and pushed verticallydown into water. When the closed end is at the water surface, how high has the water risen inside the tube ?
View Solution
Knowledge Check
A U-tube closed at one end is filled with three immiscible liquids having densities ρ,3pand8ρ as shown in figure. The pressure at point C inside the tube is:
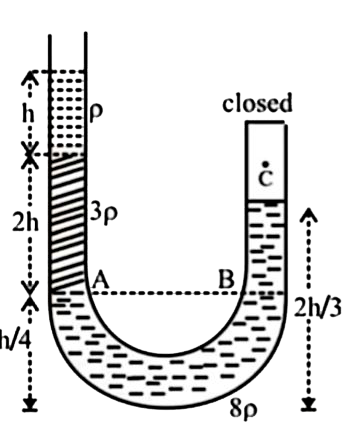 AP0+hρg3BP0+11hρg3CP0+2hρg3DP0+hρg
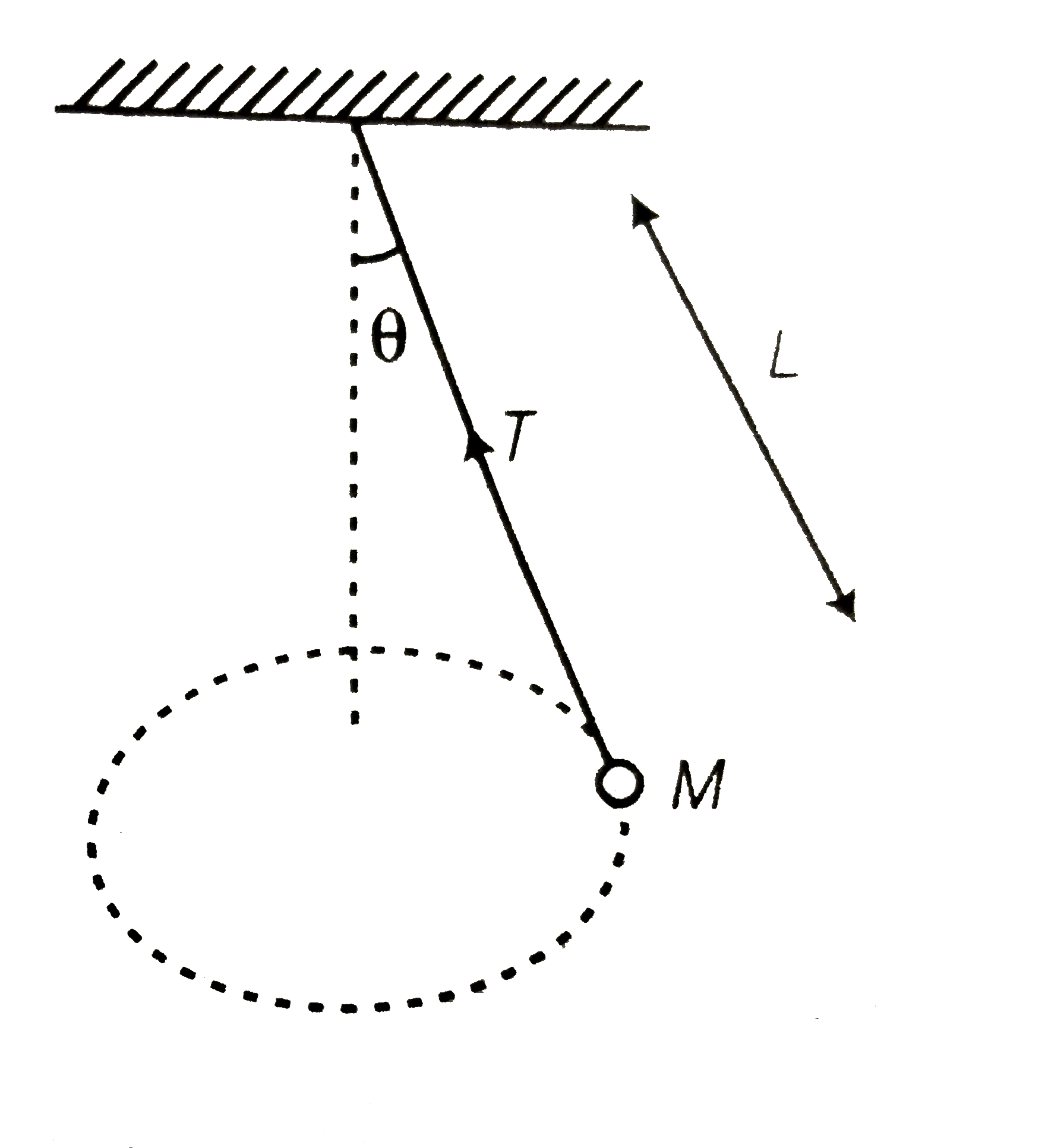
AP0+hρg3BP0+11hρg3CP0+2hρg3DP0+hρgA string of length l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
 A16 mlB4 mlC8 mlD2 ml
A16 mlB4 mlC8 mlD2 mlA tube with both ends closed has same set of natural frequency as
Aone end closed organ pipeBboth end open organ pipeCvibratory string fixed at both endsDvibratory string fixed at one end
A tube 1.5 m long and closed at on end is half filled with mercry and is then inverted with its open ends just dipping into a mercury tough.Find the height of mercury in the tube if the reading of the barometer is 0.75 m.
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2π rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
View Solution______ is a vestigial hollow tube that is closed at one end and is attached at the other end to the cecum, a pouch-like beginning of the large intestine into which the small intestine empties its contents.
View Solution______ is a vestigial hollow tube that is closed at one end and is attached at the other end to the cecum, a pouch-like beginning of the large intestine into which the small intestine empties its contents.
View SolutionA piston of mass m can move without friction in a uniform closed cylinder at one end. A gas is enclosed in it. For this situation mark the correct statement(s)
View Solution

