A uniform rectangular thin sheet ABCD of mass M has length a and breadth b, as shown in the figure. If the shaded portion HBGO is cut-off, the coordinates of the center of mass of the remaining portion will be: 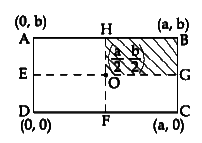
(5a3,5b3)
(5a12,5b12)
(2a3,2b3)
(3a4,3b4)
The correct Answer is:B
x=m(a4)+m(a4)+m(3a4)3m=5b12, y=m(b4)+m(b4)+m(3b4)3m=5b12.
Similar Questions
From a uniform circular plate of radius R, a small circular plate of radius R/4 is cut off as shown. If O is the center of the complete plate, then the x coordinate of the new center of mass of the remaining plate will be: X o Y
View SolutionSix rods of the same mass m and length ? are arranged as shown in figure. Calculate the coordinate of the centre of mass of the system:- У >X
View Solution
Knowledge Check
A uniform metal disc of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
AR4 from the centerBR3 from the centerCR5 from the centerDR6 from the center.A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
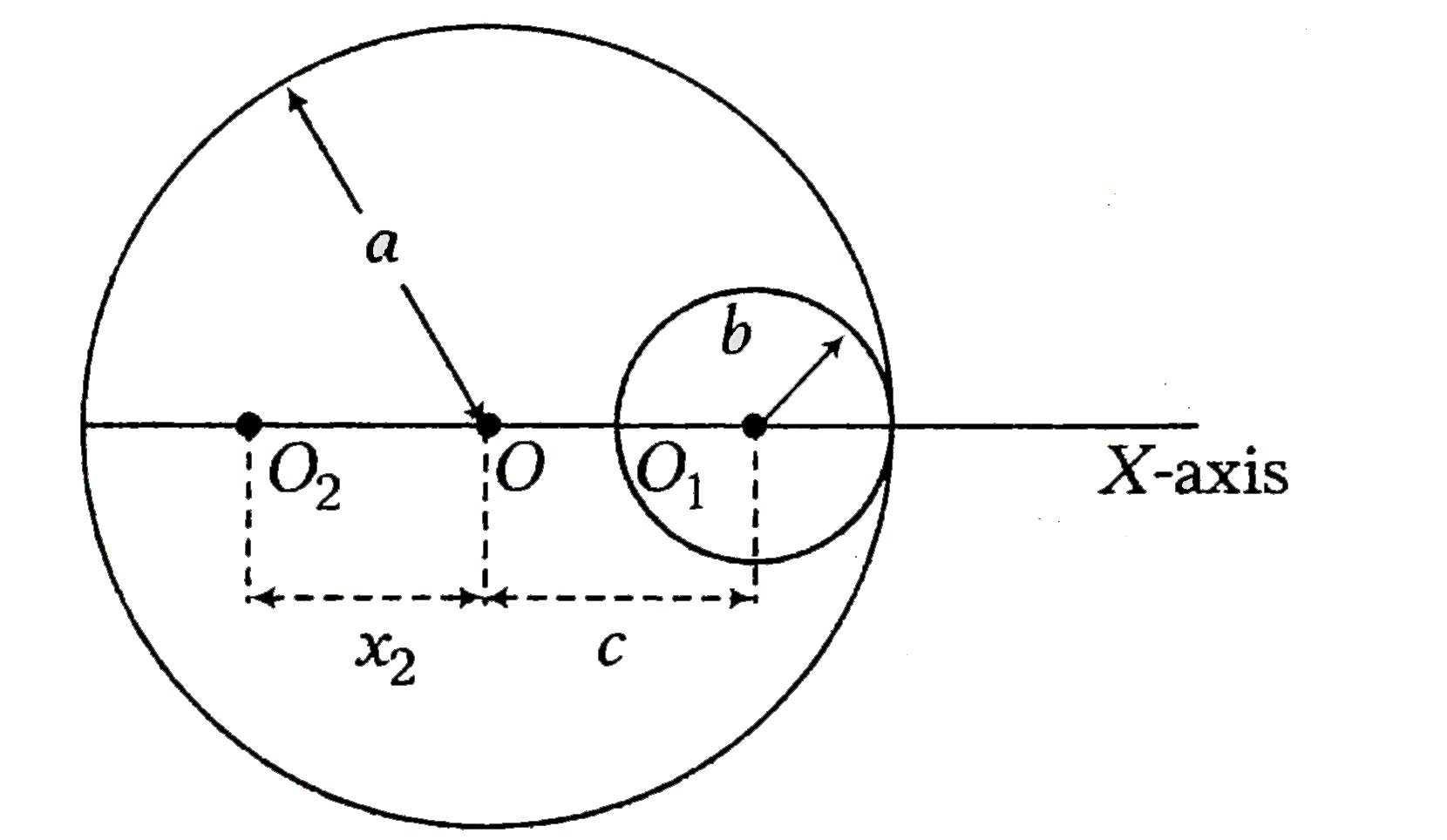 Aπb2a2−c2Bcb2a2−b2Cπc2a2−b2Dca2(c2−b2)
Aπb2a2−c2Bcb2a2−b2Cπc2a2−b2Dca2(c2−b2)A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion
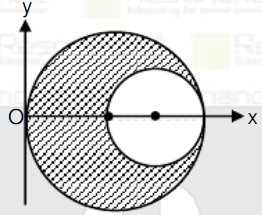
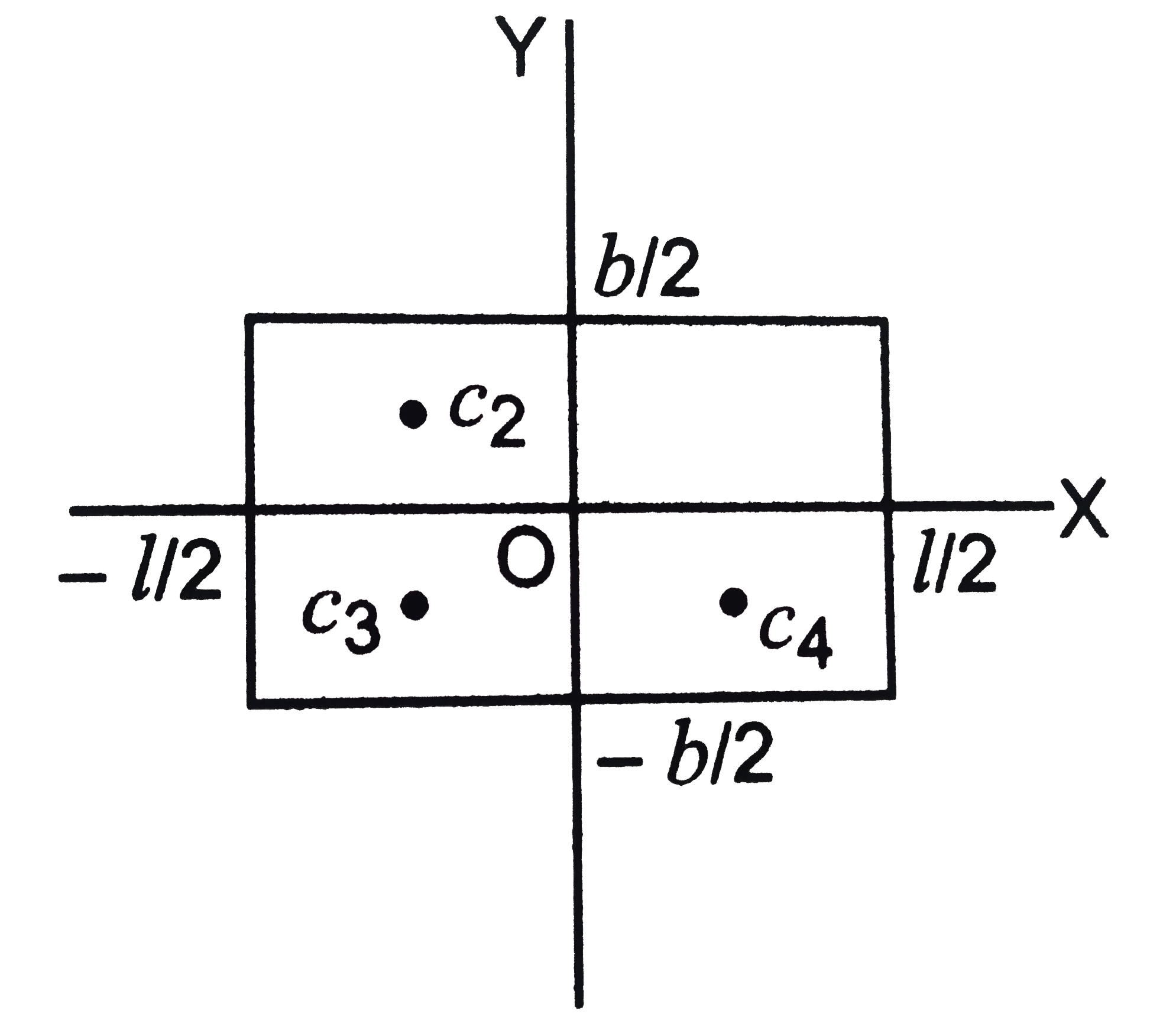
View SolutionA rectangular plate of dimensions l×b is in x−y plane as shown in Fig. If the portion of this plate lying in quadrant I is removed, find the position of centre of mass of remaining part of plate.
View SolutionA square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find
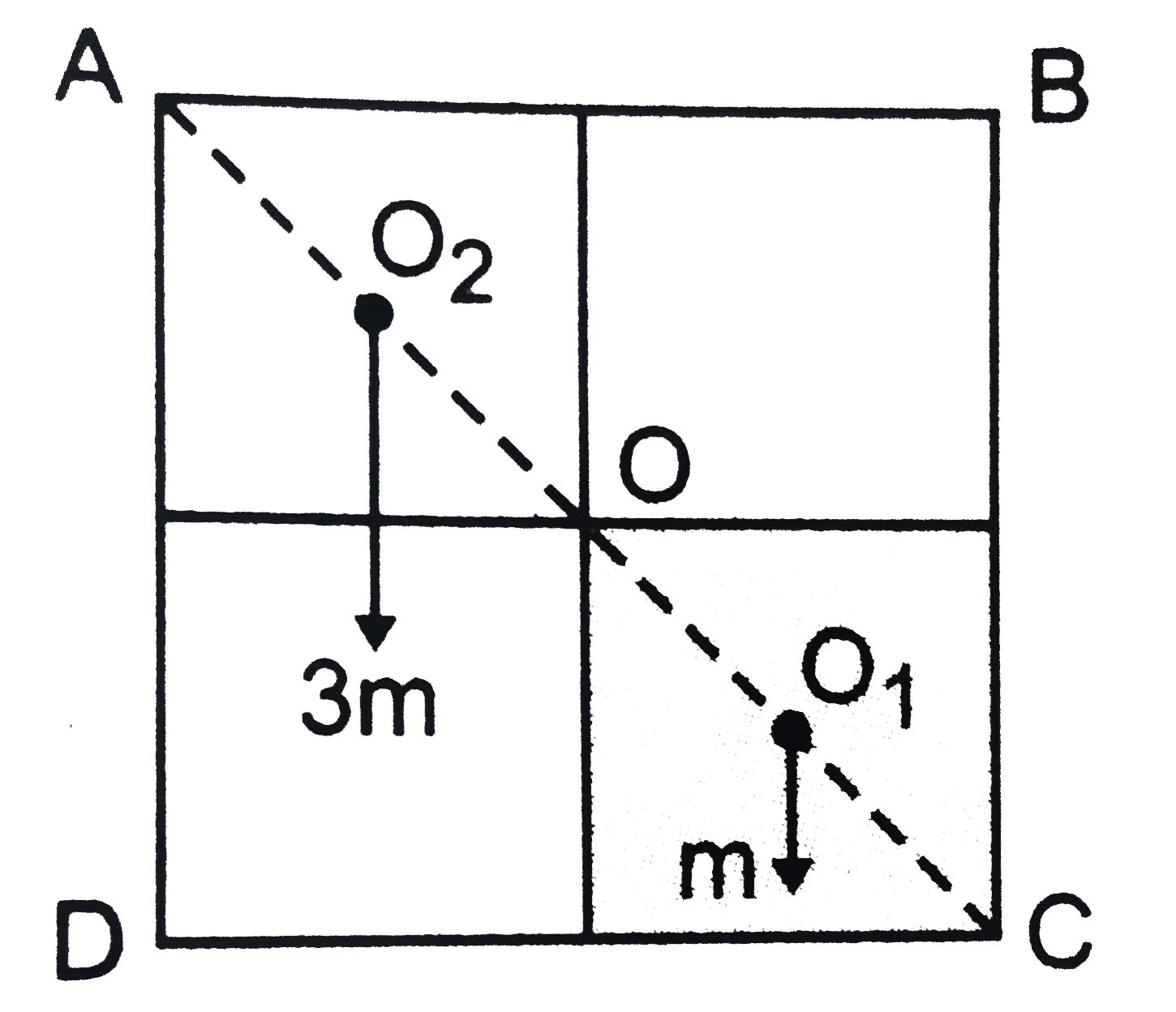
the position of centre of mass of the remaining portion from the centre O.
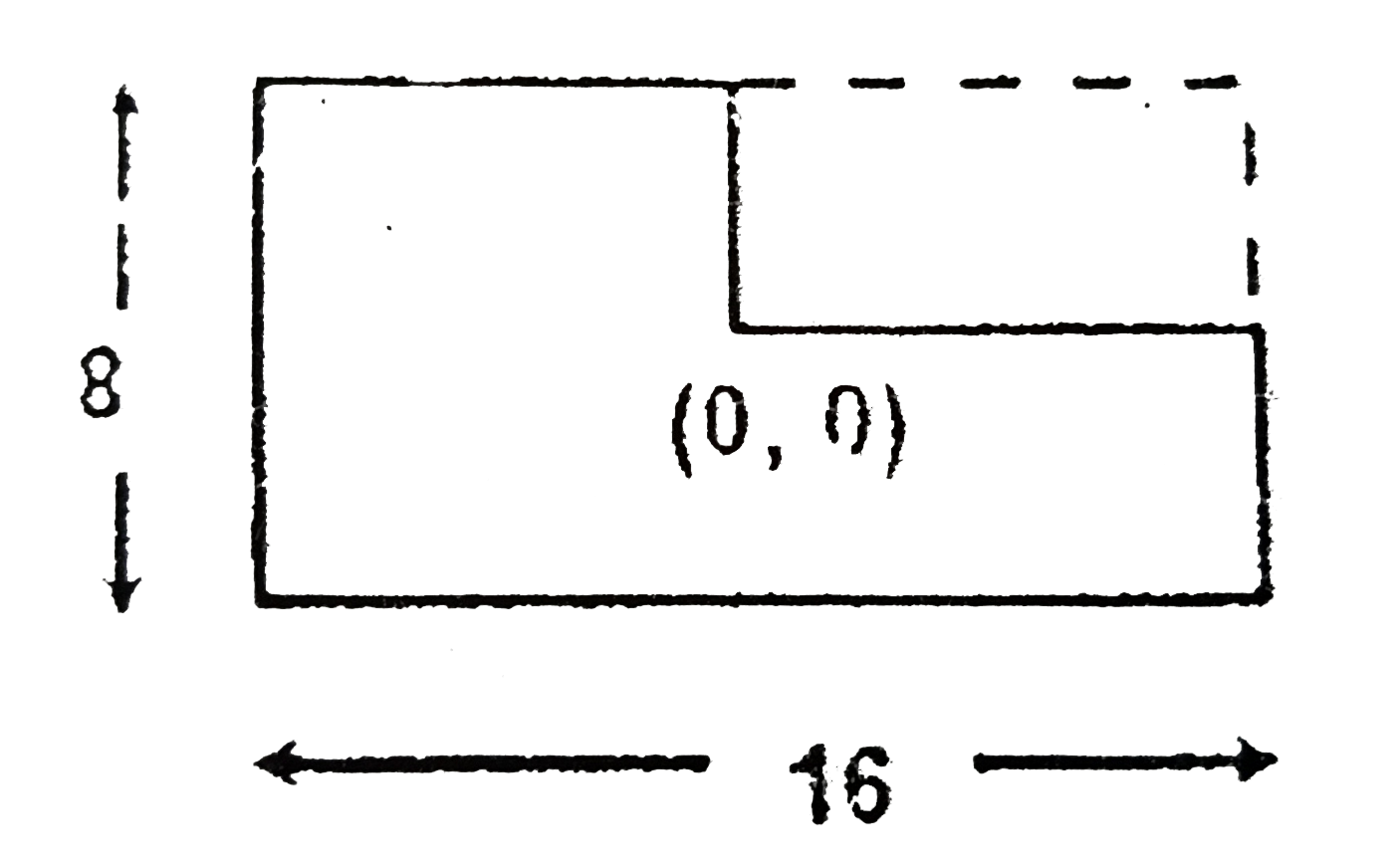
View SolutionFrom a 16cm×8cm rectangular uniform plane sheet, exactly one quarter of the sheet is removed as shown in figure. If the origin be taken at the centre of the sheet considered as shown in the figure the coordinates of the centre of mass of the remaining sheet is
View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
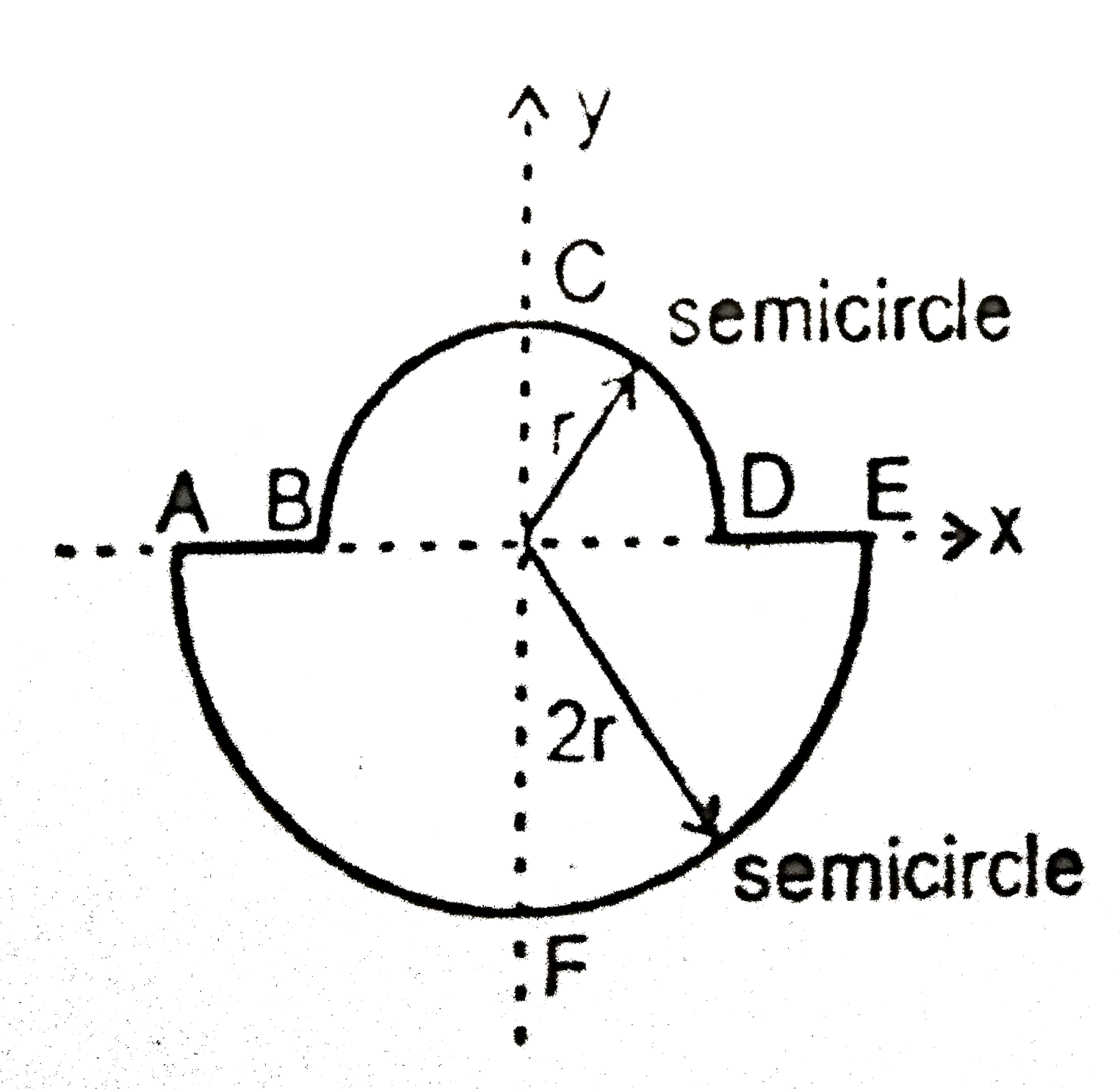
View Solution
