An elastic collision takes place between two smooth, rubber balls of same radius as shown. Initially, one ball is at rest and the other is moving with velocity u. At maximum compression :
I. Ratio of potential to initial kinetic energy of the system is $\frac{{cos}^{2} θ}{2}$
II. Ball B is moving along direction a
III. Ball A is moving along direction d
Evaluate the above statements and choose the correct option from the following:

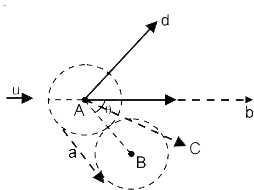
Statements I, II are true and III is false

Statements I, III are false and II is true

All statements are true

All statements are false

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Two perfectly elastic balls of same mass m are moving with velocities $u_{1}$ and $u_{2}$ . They collide elastically n times. The kinetic energy of the system finally is:
A $\frac{1}{2} \frac{m}{\cup_{1}^{2}}$
B $\frac{1}{2} \frac{m}{u} (u_{1}^{2} + u_{2}^{2})$
C $\frac{1}{2} m (u_{1}^{2} + u_{2}^{2})$
D $\frac{1}{2} m n (u_{1}^{2} + u_{2}^{2})$
A ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,

ASpeed of ball B is u $sin θ$
BVelocity of ball A is $u {sin}^{2} θ ˆ i + u sin θ cos θ ˆ j$
CSpeed of ball A is $u cos θ$
D $V e l o c i t y o f b a l l B i s$ u cos theta sin theta hati + u cos^2 theta hatj
A ball impinges directly on another ball at rest and is reduced to rest to rest b y impact. If half the initial kinetic energy is lost by impact, then the coefficient of elasticity is
A $1 / 4$
B $1 / 3$
C $3 / 4$
DNone of these