A block of mass 1 kg is moving towards a movablen vedge of amss 2 kg as shown in figure. All surfaces are smooth. When the block leaves the wedge from top, its velocity is making an angle θ=30∘ with horizontal.
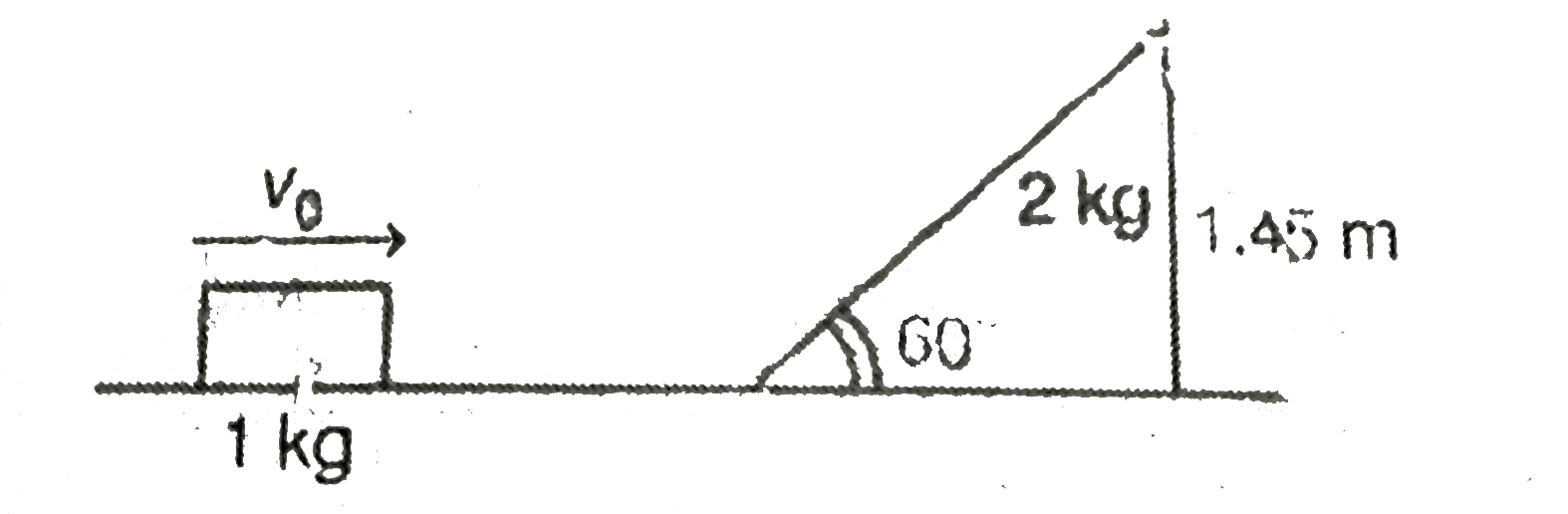
The value of v0 in m/s is
4
7
10
9
The correct Answer is:B
Let v be the horizontal velocity of wedge at topmost point and vr the relative velocity of block with respect to wedge. vr is at 60∘ with horizontal. Absolute velocity of block will be the resultant of vrandv and since it is given at 30∘ with horizontal, vrandv should be equal in magnitude.
Absolute velocity of block vb=2vcos30∘=√3v.
Now, applying conservation of linear momentum in horizontal direction and conservation of mechanical energy, we have
1×v0=2×v+1×vbcos30∘
or v0=2v+32vor v0=72v ......(1)
12×1×v20=12×2×v2+12×1×(√3v)2+1×10×1.45
or v20=2v2+3v2+29 or v20−5v2=29 ....(2)
Solving Eqs. (1) and (2), we have v0=7m/s.
Similar Questions
A block of mass 1 kg is moving towards a movablen vedge of amss 2 kg as shown in figure. All surfaces are smooth. When the block leaves the wedge from top, its velocity is making an angle θ=30∘ with horizontal.
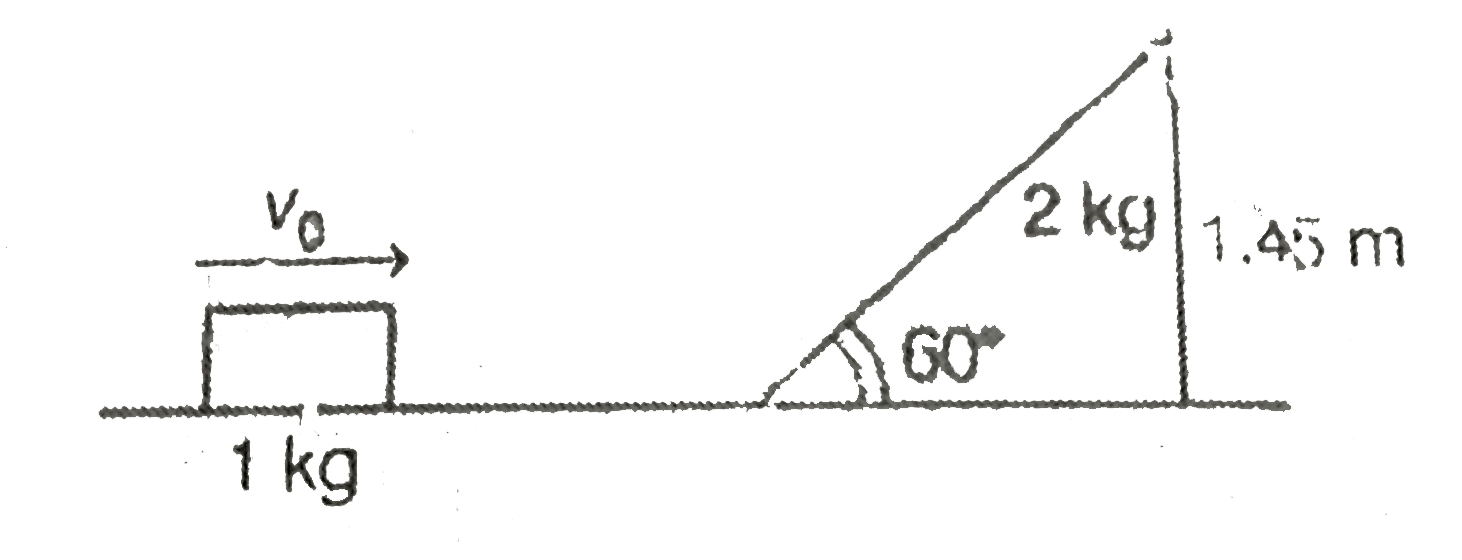
In the whole process let J be the magnitude of net impulse given to the block by the wedge, JH its horizontal component and JV its vertical component. Then
View SolutionA block of mass 1 kg is moving towards a movablen vedge of amss 2 kg as shown in figure. All surfaces are smooth. When the block leaves the wedge from top, its velocity is making an angle θ=30∘ with horizontal.

To what maximum height will the block rise
View Solution
Knowledge Check
A block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
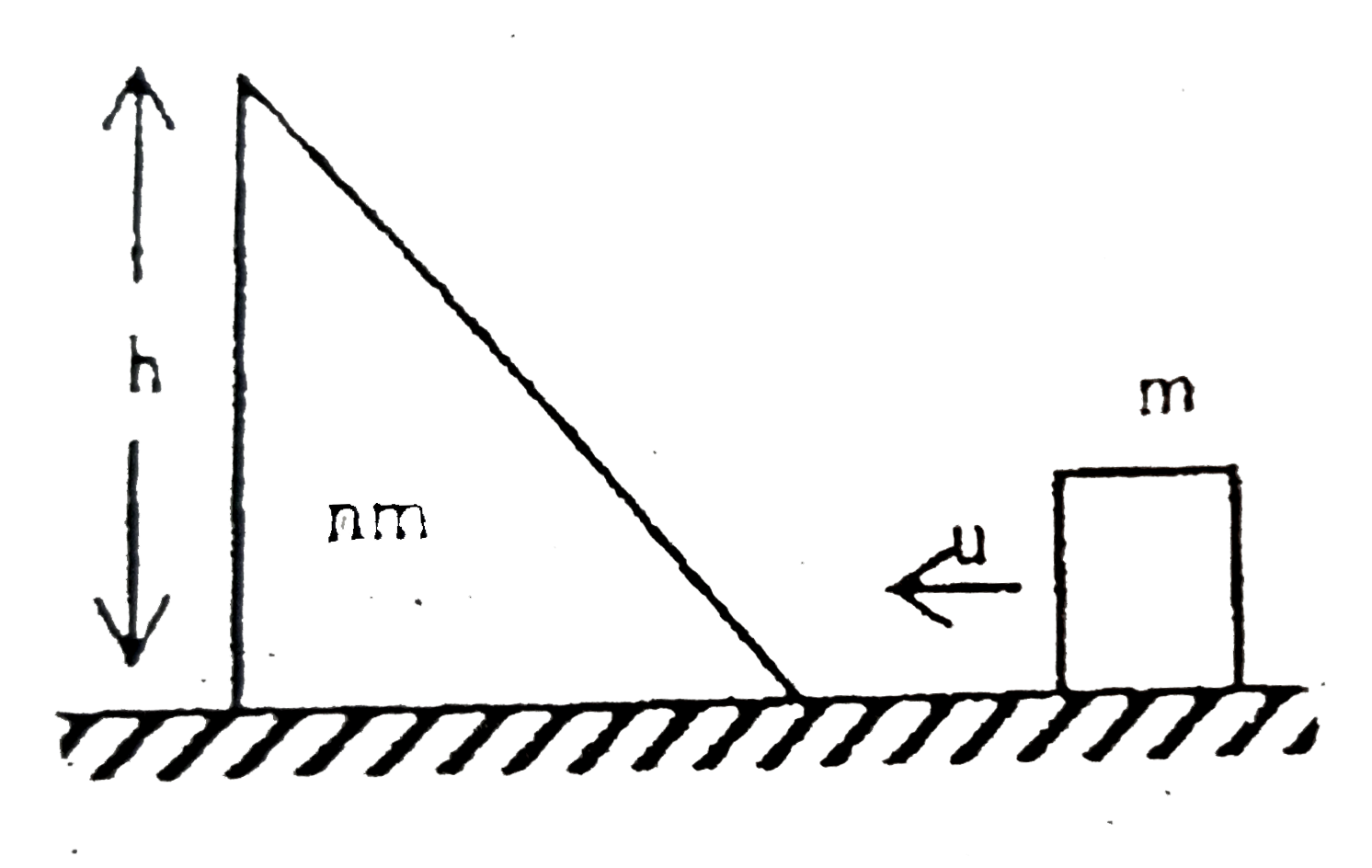 A√2ghBn2ghC√2gh(1+1n)D√2gh(1−1n)
A√2ghBn2ghC√2gh(1+1n)D√2gh(1−1n)A block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
 A√2ghB2nghC√2gh(1+1n)D√2gh(1−1n)
A√2ghB2nghC√2gh(1+1n)D√2gh(1−1n)The system of block and wedges all of same mass shown in the figure is released from rest. All surfaces are smooth. Then:
 AThe speed of block A when it falls 50cm is 2√2m/sBThe speed of block B when A falls 50cm is 4m/sCThe speed of block B when A falls 50cm is √10m/sDThe speed of block C when A falls 50cm is √2m/s
AThe speed of block A when it falls 50cm is 2√2m/sBThe speed of block B when A falls 50cm is 4m/sCThe speed of block B when A falls 50cm is √10m/sDThe speed of block C when A falls 50cm is √2m/s
A block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
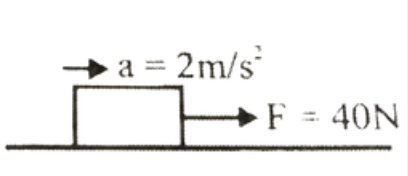
View SolutionA small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
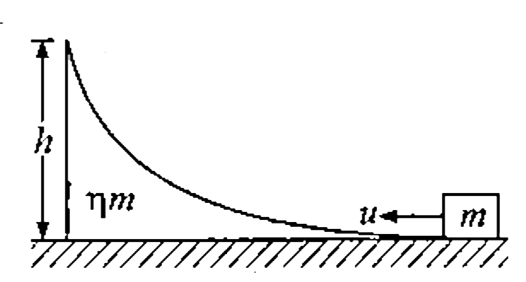
View SolutionA small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:

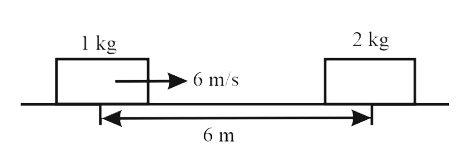
View SolutionA block of mass 1 kg is pushed towards another block of mass 2 kg from a 6 m distance as shown in the figure. If just after the collision, the velocity of 2 kg block is 4ms−1, then
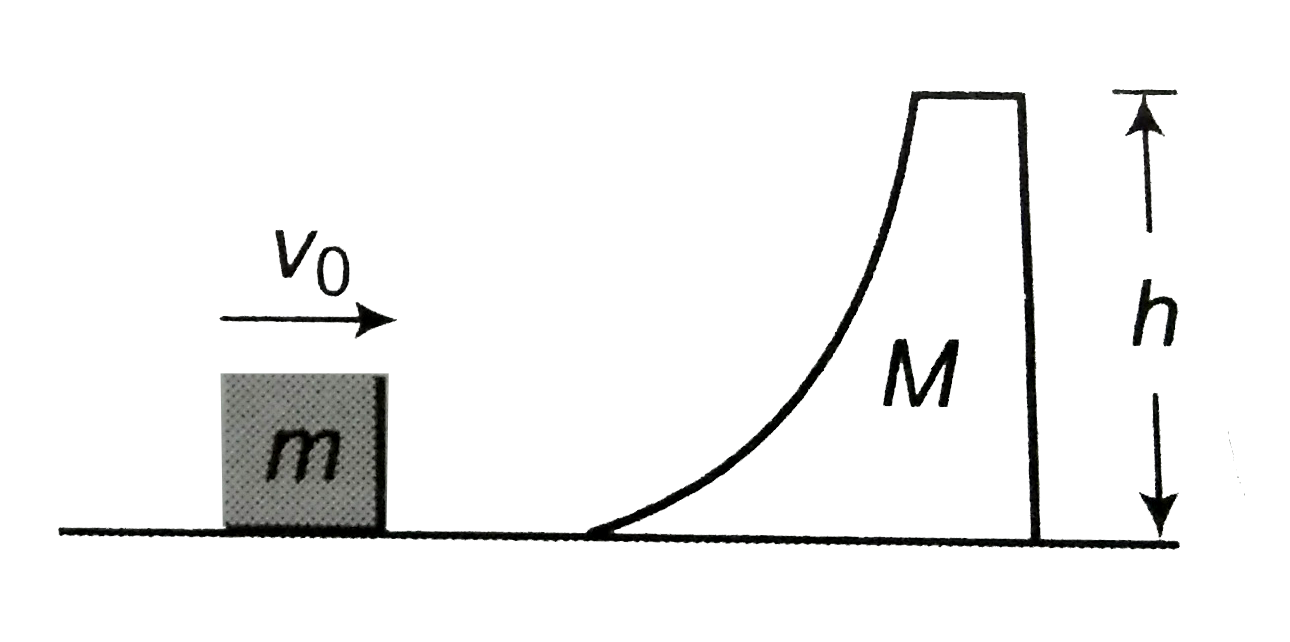
View SolutionA block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
View Solution

