The displacement of a particle of mass 2kg moving in a straight line varies with times as x=(2t3+2)m. Impulse of the force acting on the particle over a time interval between t = 0 and t = 1 s is
10N−s
12N−s
8N−s
6N−s
The correct Answer is:B
S=2t3+2, V=dsdt=6t2
⇒a=dVdt=12t⇒F=ma=24t, I=∫Fdt=∫1024tdt=[12t2]10=12N−s .
Similar Questions
The position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is

View Solution
Knowledge Check
Kinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
Ais constantBis increasingCis decreasingDfirst increase and then decreasesKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
ADirectly proportional to the speed of the particleBInversely proportional to √tCInversely proportional to the speed of the particleDDirectly proportional to √tThe position of a particle moving on a straight line depends on time t as
x=(t+3)sin(2t)AIts velocity at the initial moment is 6 m/sBIts acceleration at the initial is −8m/s2CIt has velocity of 3 m/s at t=π2 secDIt has an acceleration of 2m/s2 at t=π4 sec
Velocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
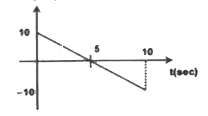
View SolutionThe displacement 'x' of a particle moving along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is :-
View SolutionA particle of mass 10 kg is moving in a straight line. If its displacement, x with time tis given by x=(t3−2t−10)m then the force acting on it at the end of 4 seconds is
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
View Solution