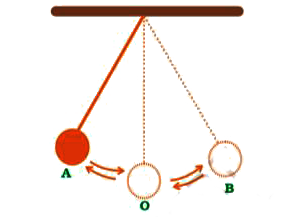
A simpel pendulum is vibrating with an angular amplitdue of as shown in figure, then:

θ=0, acceleration directed downward
θ=0,acceleration directed upward
θ=90∘, acceleration directed downward
θ=cos−1(1√3),acceleration directed horizontal
The correct Answer is:B, C, D
At θ=90∘,v=0,
∴an=v2r=0andat=gsin90∘=g
At any angular position θ,h=1cosθ ∴ v2=2ghI
an=v2r=2glcosθl=2gcosθandat=gsinθ
Thus tanθ=axat or sinθcosθ=2gcosθgsinθ or 2cos2θ=sin2θ=1−cos2θ
cosθ=1√3
Similar Questions
Knowledge Check
A simple pendulum is vibrating with an angular amplitude of 90∘ as shown in figure. For what value of α (angle between string and vertical) during its motion, the total acceleration is directed horizontally ?
 Atan−1(12)Btan−1(1√2)Ccos−1(1/√3)Dsin−2(1/√3)
Atan−1(12)Btan−1(1√2)Ccos−1(1/√3)Dsin−2(1/√3)A simple pendulum is vibrating with an angular amplitude of 90∘ as shown in the figure. For what value of a is the acceleration directed

i) vertically upwards
ii) horizontally
iii) vertically downwardA0∘,cos−1(1√3),90∘B90∘,cos−1(1√3),0∘Ccos−1(1√3),0∘,90∘Dcos−1(1√3),90∘,0∘A simple pendulum is oscillating with an angular amplitude of 90∘ as shown in the figure. The value of θ for which the resulting acceleration of the bob is directed (i) vertically downward, (ii) vertically upward and (iii) horizontally is
 A90∘,0∘,sin−1(1/√3)B0∘,90∘,sin−1(1√3)C90∘,0∘,cos−1(1/√3)D0∘,90∘,cos−1(1/√3)
A90∘,0∘,sin−1(1/√3)B0∘,90∘,sin−1(1√3)C90∘,0∘,cos−1(1/√3)D0∘,90∘,cos−1(1/√3)
A simple pendulum is vibrating in an evacuated chamber. It will
View Solutiona simple pendulum with a bob of mass m savings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the strings is-
View Solution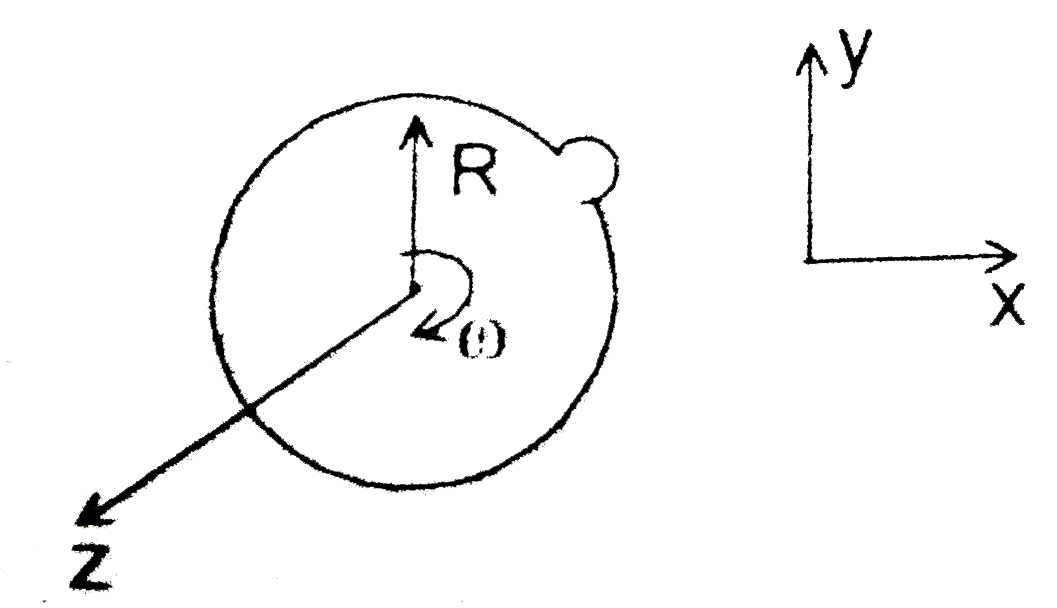
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.
View SolutionA simple pendulum is vibrating in an evacuated chamber, it will oscillate with
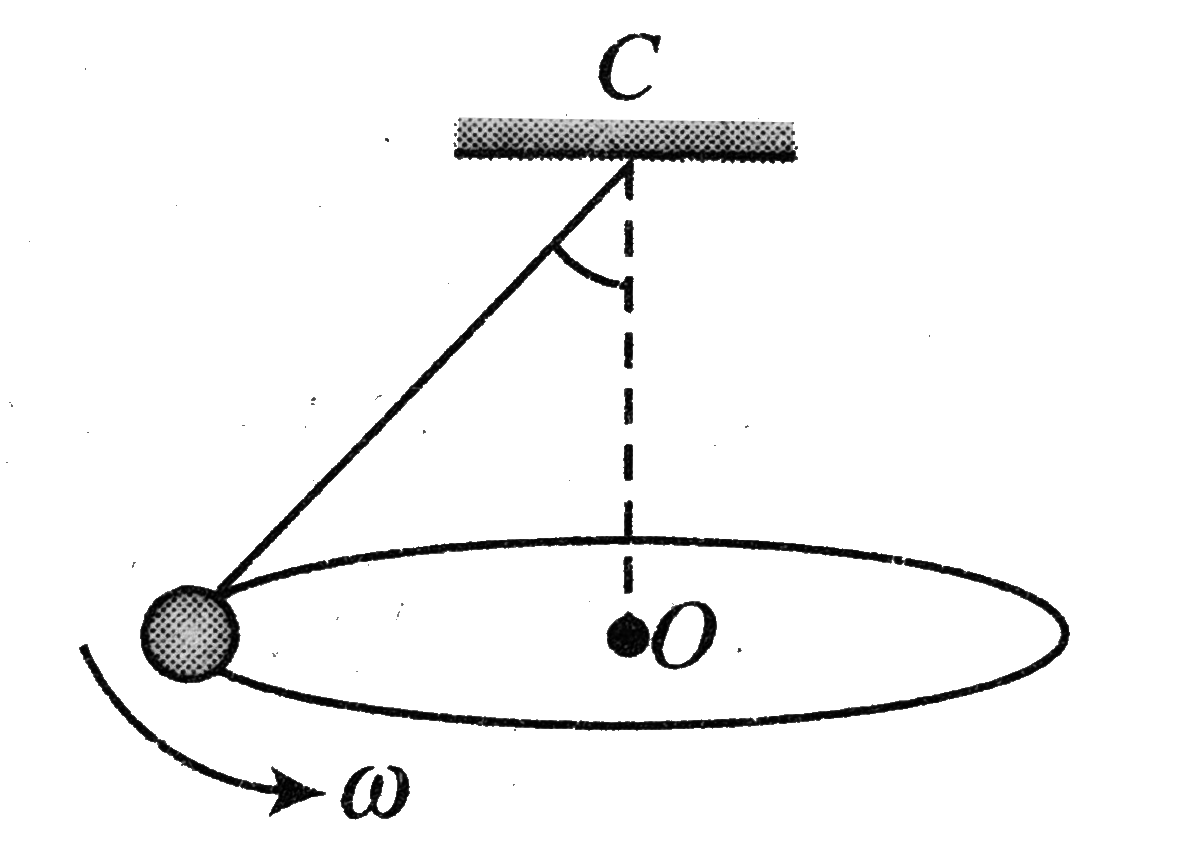
View SolutionA conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
View Solution