A particle of mass m moving with a velocity u makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extermely small time. T. Their force of contact increases from zero to F0 linearly in time T/4, remains constant for a further time T/2 and decreases linearly from F0 to zero in further time T/4 as shown. The magnitude possessed by F0 is.
 .
.
muT
2muT
4mu3T
3mu4T
The correct Answer is:C
Impulse on particle m = Area under F−tcurve=F0(T+T2)2=m(0−u)
∴F0=4mu3T.
Similar Questions
A body of mass 1kg moving with velocity 1ms makes an elastic one dimensional collision with an identical stationary body. They are in contact for brief time 1(~s). Their force of interaction increases from zero to F0 linearly in time 0.5s and decreases linearly to zero in further time 0.5s as shown in the figure. The magnitude of force F0 (in newton) is
'(##CEN_KSR_PHY_JEE_C08_E01_009_Q05##)'
View SolutionA body of mass 1kg moving with velocity 1m/s makes an elastic one dimesional collision with an identical stationary body. They are in contact for brief time 1sec. Their force of interaction increases form zero to F0 linearly in time 0.5s and decreases linearly to zero in further time 0.5sec as shown in figure. Find the magnitude of force F0 in newton.
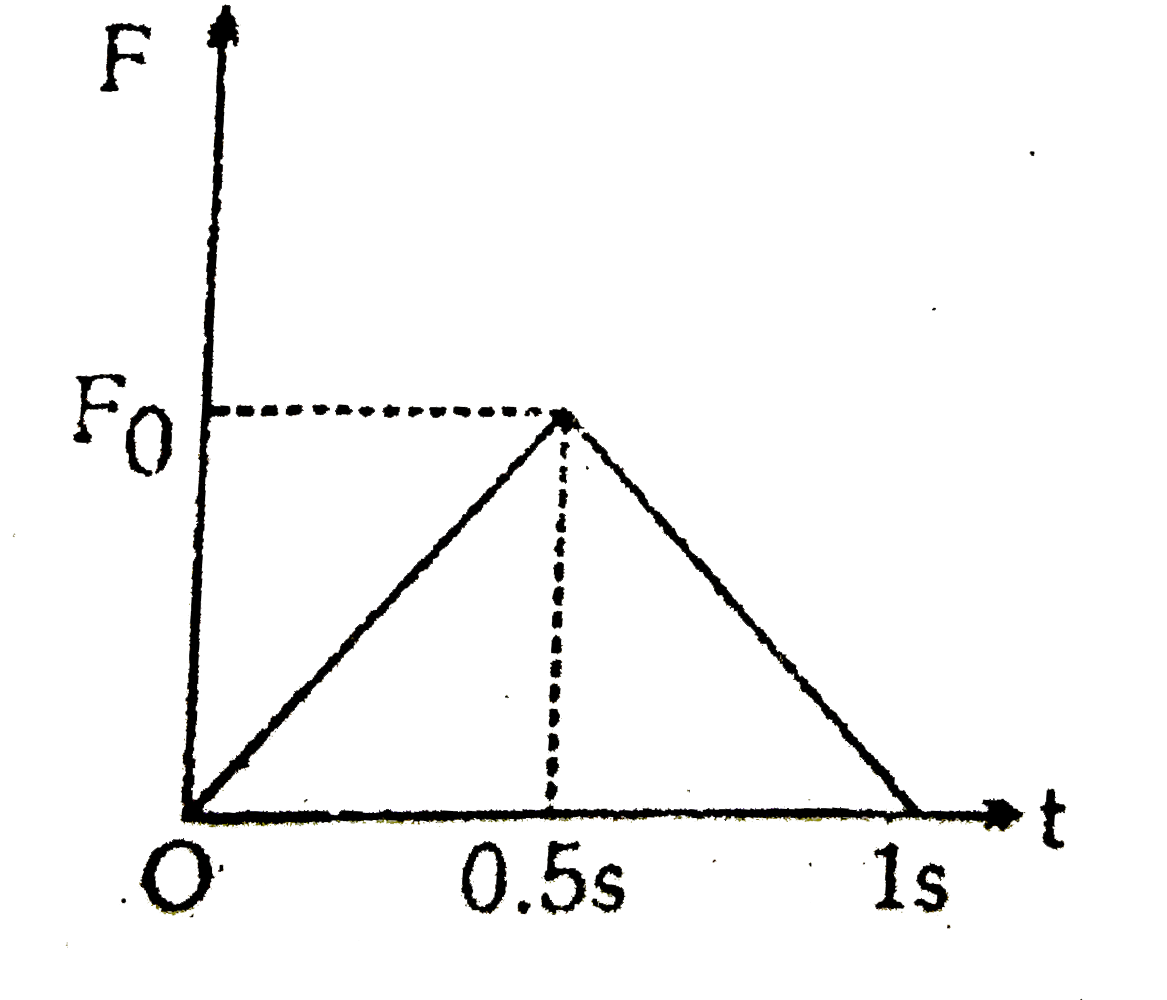
View Solution
Knowledge Check
A particle of mass m moving with velocity u makes an elastic one-dimensional collision with a stationary particle of mass m. They come in contact for a very small time t0. Their force of interaction increases from zero to F0 linearly in time 0.5t0, and decreases linearly to zero in further time 0.5t0 as shown in figure. The magnitude of F0 is
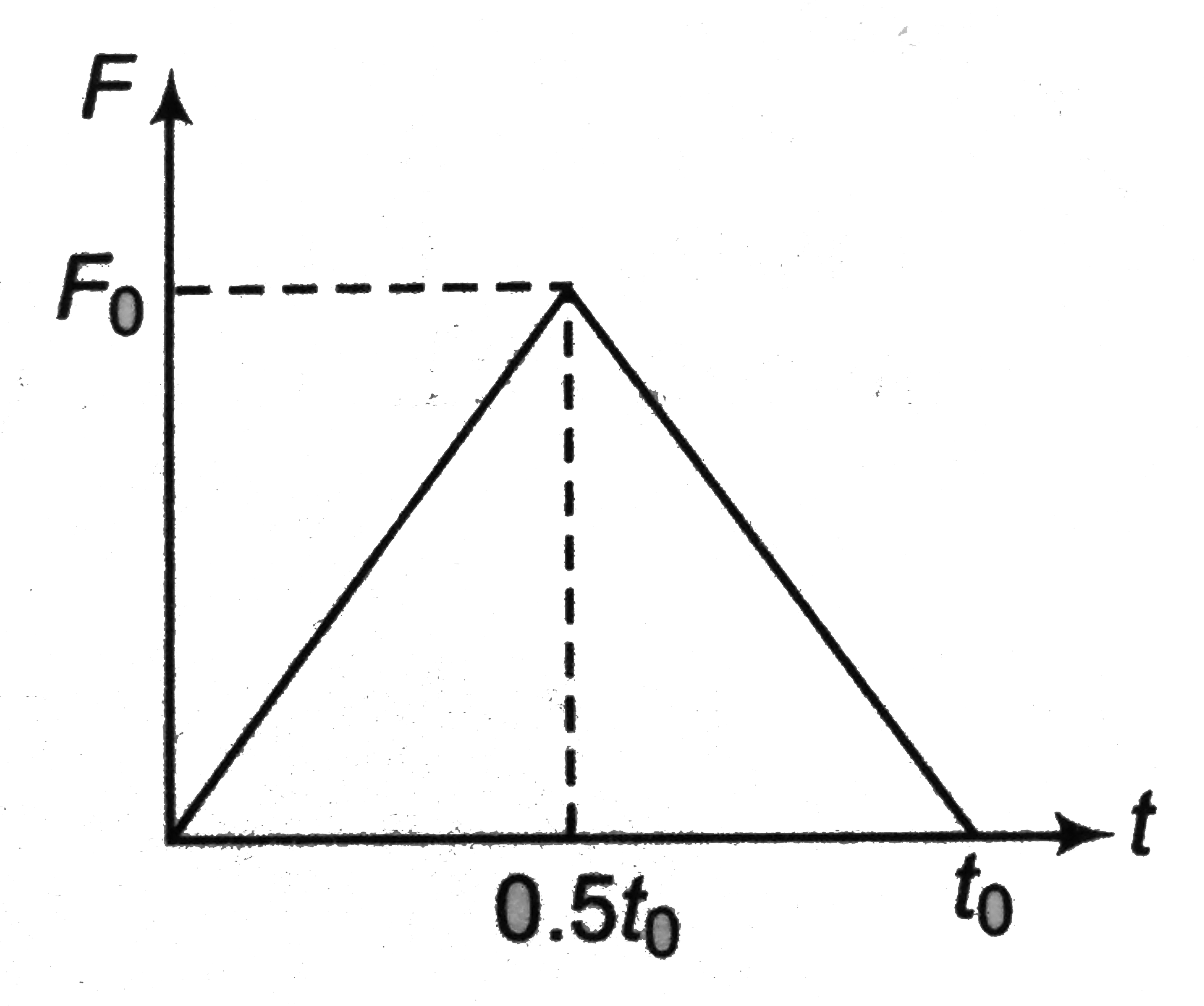 Aμt0B2μt0Cμ2t0DNone of these
Aμt0B2μt0Cμ2t0DNone of theseA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
AF2t2mBF2t22mCF2t23mDFt2mA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2m
A particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the

View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA constant force (F) is applied on a stationary particle of mass 'm'. The velocity attained by the particle in a certain interval of time will be proportional to
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View Solution
