In two containers X and Y same gas is filled. If the pressure, volume and absolute temperature of gas in X are three times as compared to that in Y and if the mass of X is mg, the mass of Y is
mg
m/3g
m/2g
2mg
The correct Answer is:B
To solve the problem, we need to analyze the conditions given for the two containers X and Y filled with the same gas. We will use the Ideal Gas Law, which states that:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = absolute temperature
1. Identify the conditions for containers X and Y:
- For container X:
- Pressure PX=3PY
- Volume VX=3VY
- Temperature TX=3TY
- For container Y:
- Pressure PY=P
- Volume VY=V
- Temperature TY=T
2. Apply the Ideal Gas Law for container X:
PXVX=nXRTX
Substituting the values:
(3P)(3V)=nXR(3T)
Simplifying:
9PV=3nXRT
Dividing both sides by 3:
3PV=nXRT(Equation 1)
3. Apply the Ideal Gas Law for container Y:
PYVY=nYRTY
Substituting the values:
PV=nYRT(Equation 2)
4. Relate the number of moles to mass:
The number of moles n can be expressed in terms of mass m and molar mass M:
n=mM
For container X:
nX=mM(mass of gas in X is m grams)
For container Y:
nY=mYM(mass of gas in Y is mY grams)
5. Substituting the expressions for nX and nY into Equations 1 and 2:
- From Equation 1:
3PV=mMRT
- From Equation 2:
PV=mYMRT
6. Equate the two equations:
Since both equations equal PV:
3PV=mMRTandPV=mYMRT
Dividing the first equation by the second:
3PVPV=mmY
This simplifies to:
3=mmY
Rearranging gives:
mY=m3
Final Answer:
The mass of gas in container Y is m3 grams.
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = absolute temperature
- For container X:
- Pressure PX=3PY
- Volume VX=3VY
- Temperature TX=3TY
- For container Y:
- Pressure PY=P
- Volume VY=V
- Temperature TY=T
PXVX=nXRTX
Substituting the values:
(3P)(3V)=nXR(3T)
Simplifying:
9PV=3nXRT
Dividing both sides by 3:
3PV=nXRT(Equation 1)
PYVY=nYRTY
Substituting the values:
PV=nYRT(Equation 2)
The number of moles n can be expressed in terms of mass m and molar mass M:
n=mM
For container X:
nX=mM(mass of gas in X is m grams)
For container Y:
nY=mYM(mass of gas in Y is mY grams)
- From Equation 1:
3PV=mMRT
- From Equation 2:
PV=mYMRT
Since both equations equal PV:
3PV=mMRTandPV=mYMRT
Dividing the first equation by the second:
3PVPV=mmY
This simplifies to:
3=mmY
Rearranging gives:
mY=m3
The mass of gas in container Y is m3 grams.
Topper's Solved these Questions
- STATE OF MATTER (GASEOUS AND LIQUID STATE)BOOK - DINESH PUBLICATIONCHAPTER - STATE OF MATTER (GASEOUS AND LIQUID STATE)EXERCISE - Revision question from competitive exams
147 Videos
- STATE OF MATTER (GASEOUS AND LIQUID STATE)BOOK - DINESH PUBLICATIONCHAPTER - STATE OF MATTER (GASEOUS AND LIQUID STATE)EXERCISE - Selected straight objective types MCQs
58 Videos
- S-BLOCK ELEMENTS (ALKALI AND ALKALINE EARTH METALS )BOOK - DINESH PUBLICATIONCHAPTER - S-BLOCK ELEMENTS (ALKALI AND ALKALINE EARTH METALS )EXERCISE - Assertion reason
12 Videos
- STATES OF MATTER (SOLID STATE CHEMISTRY)BOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER (SOLID STATE CHEMISTRY)EXERCISE - ULTIMATE PREPARATORY PACKAGE
21 Videos
Similar Questions
A gas is filled in a container at certain temperature and pressure. At the same temperature more gas is filled in the vessel. Calculate the percentage increase in the mass of the gas. If the ratio of initial and final pressure is 1:2.
View SolutionA gas is filled in a container at certain temperature and pressure. At the same temperature more gas is filled in the vessel. Calculate the percentage increase in the mass of the gas. If the ratio of initial and final pressure is 1:2.
View Solution
Knowledge Check
Two vessels A and B contain the same gas. If the pressure, volume and absolute temperature of the gas in A are two times as compared to that in B, and if the mass of the gas in B is x grams, the mass of the gas in A will be
A4x gBx2 gC2x gDx gIf the absolute temperature of a gas is doubled and the pressure is reuced to one-half, the volume of the gas will ____________
ARemain unchangedBBe doubledCIncrease four-foldDBe reduced to 1/4thA ideal gas has pressure 'p', volume 'V' and absolute temperature 'T'. It 'm' is the mass of each molecules and 'K' is the Boltzmann constant , the density of the gas is
ApmMTBKTpmCKmpTDpKTm
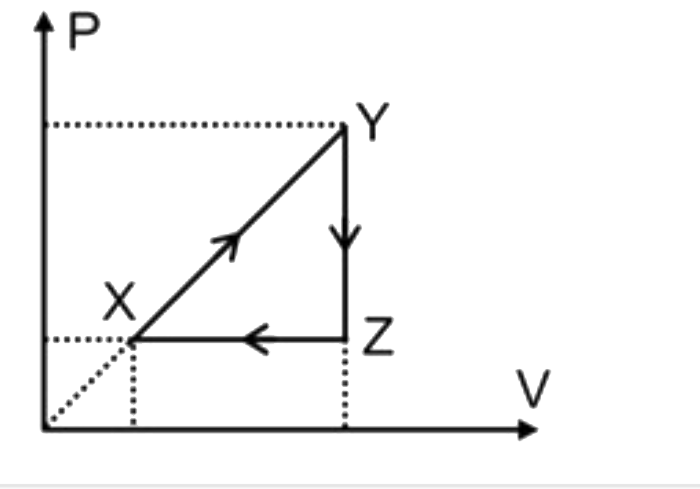
In the show indicator diagram over pressure - volume scales 'n' moles of an ideal gas is cycled . If the temperature of the gas in the state X and Y are respectively TXandTY . Temperature of the gas in the state Z is the (All temperature are in absolute scale )
View SolutionIf the absolute temperature of a gas is doubled and the pressure is reuced to one-half, the volume of the gas will ____________
View SolutionA gas is undergoing an adiabatic process. At a certain stage, the volume and absolute temperature of the gas are V0,T0 and the magnitude of the slope of the V-T curve is m. molar specific heat of the gas at constant pressure is [Assume the volume of the gas is taken on the y-axis and absolute temperature of the gas taken on x-axis]
View SolutionA container X has volume double that of container Y and both are connected by a thin tube. Both contains same ideal gas. The temperature os X is 200K and that of Y is 400K. If mass of gas in X is m then in Y it will be.
View SolutionIf the volume of a given mass of a gas at constant temperature becomes three times, the pressure will be
View Solution
