Prove that the triangle of maximum area that can be incsribed in a given circle is an equilateral triangle.Solution in Bengali
Step by step video & image solution for Prove that the triangle of maximum area that can be incsribed in a given circle is an equilateral triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAXIMA AND MINIMA Book:CHHAYA PUBLICATIONChapter:MAXIMA AND MINIMA Exercise:Sample Questions for Competitive Examination A
Explore 5 Videos
- MAXIMA AND MINIMA Book:CHHAYA PUBLICATIONChapter:MAXIMA AND MINIMA Exercise:Sample Questions for Competitive Examination B
Explore 5 Videos
- MAXIMA AND MINIMA Book:CHHAYA PUBLICATIONChapter:MAXIMA AND MINIMA Exercise:EXERCISE Short Answer Type Questions
Explore 42 Videos
- MATHEMATICAL REASONING Book:CHHAYA PUBLICATIONChapter:MATHEMATICAL REASONING Exercise:JEE Main (AIEEE) Archive (2016 )
Explore 1 Video
- MCQ ZONE Book:CHHAYA PUBLICATIONChapter:MCQ ZONE Exercise:Question Paper 7
Explore 80 Videos
Similar Questions
The function f(x)=sinxcos2x has extremum at -
View SolutionThe maximum value of 7e|xlogx| for 0<x≤1 is-
View SolutionDivide 24 into two parts such that their product is maximum.
View SolutionThe boolean expression (p∧~q)∨q∨(~p∧q) is equivalent to
View SolutionThe inverse of the matrix ⎡⎢⎣100a10bc1⎤⎥⎦ is -
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View Solutionसिद्ध कीजिये कि किसी दिये हुए वृत में अधिकतम क्षेत्रफल वाला त्रिभुज समबाहु त्रिभुज होता है ।
View Solutionसिद्ध कीजिये कि किसी वृत्त में अधिकतम क्षेत्रफल वाला अंत : त्रिभुज समबाहु होता है ।
View Solutionसिद्ध कीजिए कि किसी व्रत में अधिकतम क्षेत्रफल वाला अतःत्रिभुज समबाहु होता है।
View Solution△PQR একটি সমবাহু ত্রিভুজ। ∠QER=?
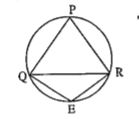
View Solutionthe area of an equilateral triangle is .
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View SolutionGiven the perimeter of a triangle, prove that the triangle of the greatest area is equilateral.
View Solution

