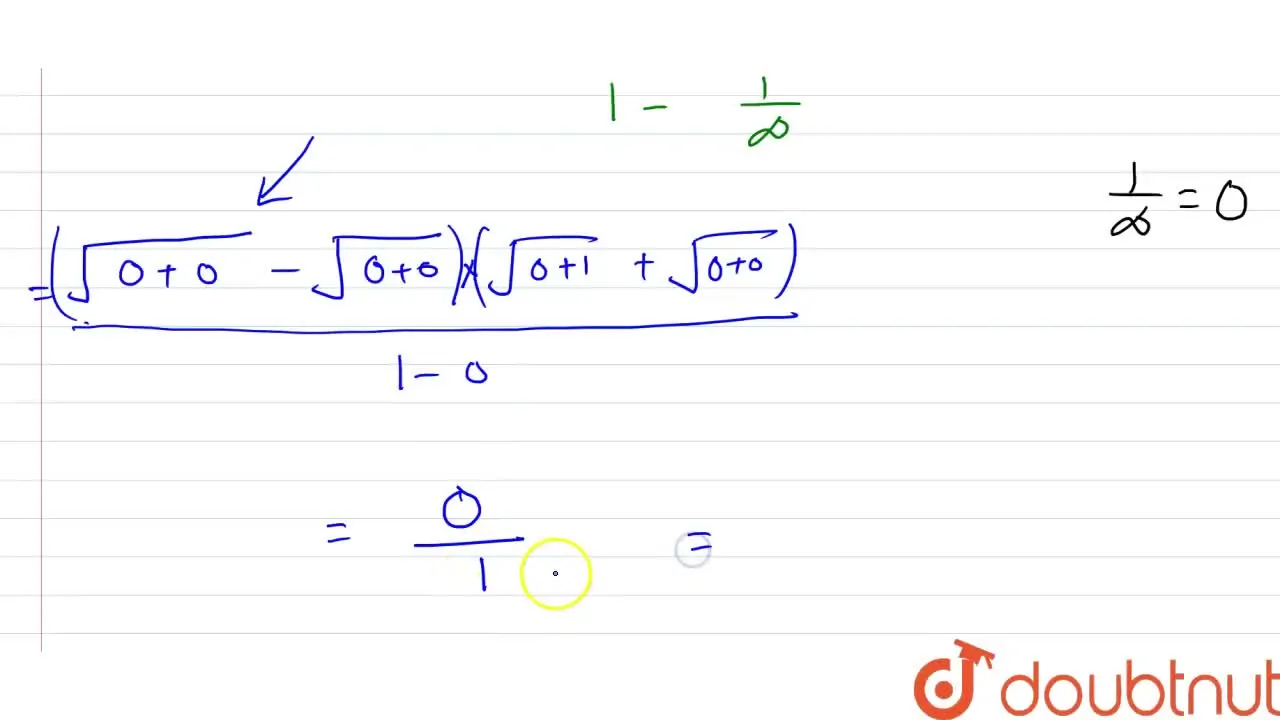
Evaluate :
limn→∞√1+n2−√1+n√1+n3−√1+nSolution in Bengali
The correct Answer is:0
Step by step video & image solution for Evaluate : underset(nrarroo)"lim"(sqrt(1+n^(2))-sqrt(1+n))/(sqrt(1+n^(3))-sqrt(1+n)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - CHHAYA PUBLICATIONCHAPTER - LIMITEXERCISE - EXERCISE 2 ( Long Answer Type Questions)38videos
LIMIT
- BOOK - CHHAYA PUBLICATIONCHAPTER - LIMITEXERCISE - Sample Questions for Competitive Exams (Multiple Correct Answers Type )5videos
LIMIT
- BOOK - CHHAYA PUBLICATIONCHAPTER - LIMITEXERCISE - EXERCISE 2 (Very Short Answer Type Questions )56videos
LIMIT
- BOOK - CHHAYA PUBLICATIONCHAPTER - LAWS OF INDICESEXERCISE - Long Answer Type Questions6videos
LAWS OF INDICES
- BOOK - CHHAYA PUBLICATIONCHAPTER - LINEAR DIFFERENTIAL EQUATION EXERCISE - Sample Question for Competitive Examination(E. Assertion-Reason Type)2videos
LINEAR DIFFERENTIAL EQUATION
Similar Questions
Draw the graph of the function y=x2x and from the graph evaluate limx→0x2x
03:32View Solutionlimn→∞−3n+(−1)n4n−(−1)n is equal to
05:33View SolutionEvaluate the following limits: limx→1(√2−x−11−x)
03:11View Solution6(4x+9x)=13.6x
03:23View SolutionConsider the differential equation dydx=y2ylogy+y−x.
Statement - I xy=y2logy+c is a solution of the given differential equation.
Statement - II : The differental equation is a linear equation in y and x.02:20View SolutionFor all n in N,1+(1)/(sqrt(2))+(1)/(sqrt(3))+(1)/(sqrt(4))++(1)/(sqrt(n))
02:13View Solutionlimn→∞⎡⎢ ⎢⎣1n+√n2−12n2+√n2−22n2+...+√n2−(n−1)2n2⎤⎥ ⎥⎦
02:03View Solutionlimn→∞⎧⎪ ⎪⎨⎪ ⎪⎩1√n2+1√n2−12+1√n2−22+...+1√n2−(n−1)2⎫⎪ ⎪⎬⎪ ⎪⎭ is equal to-
04:27View Solutionlimn→∞(√n4+1−√n4−1)=
04:19View SolutionFind limn→∞√n2+1+√n√n2+1−√n
02:22View SolutionEvaluate :
limn→∞1+√n1−√n04:01View SolutionProve : limn→∞(√n+1−√n)=0
05:26View SolutionFind the value of
limn→∞⎡⎢ ⎢⎣1√n2−12+1√n2−22+1√n2−32+...+1√n2−(n−1)2⎤⎥ ⎥⎦03:50View SolutionEvaluate (with the help of definite integral) :
limn→∞[1√n+1√2n+1√3n+…+1n]04:41View Solutionlimn→∞√1+√2+…+√n−1n√n=
11:18View Solution