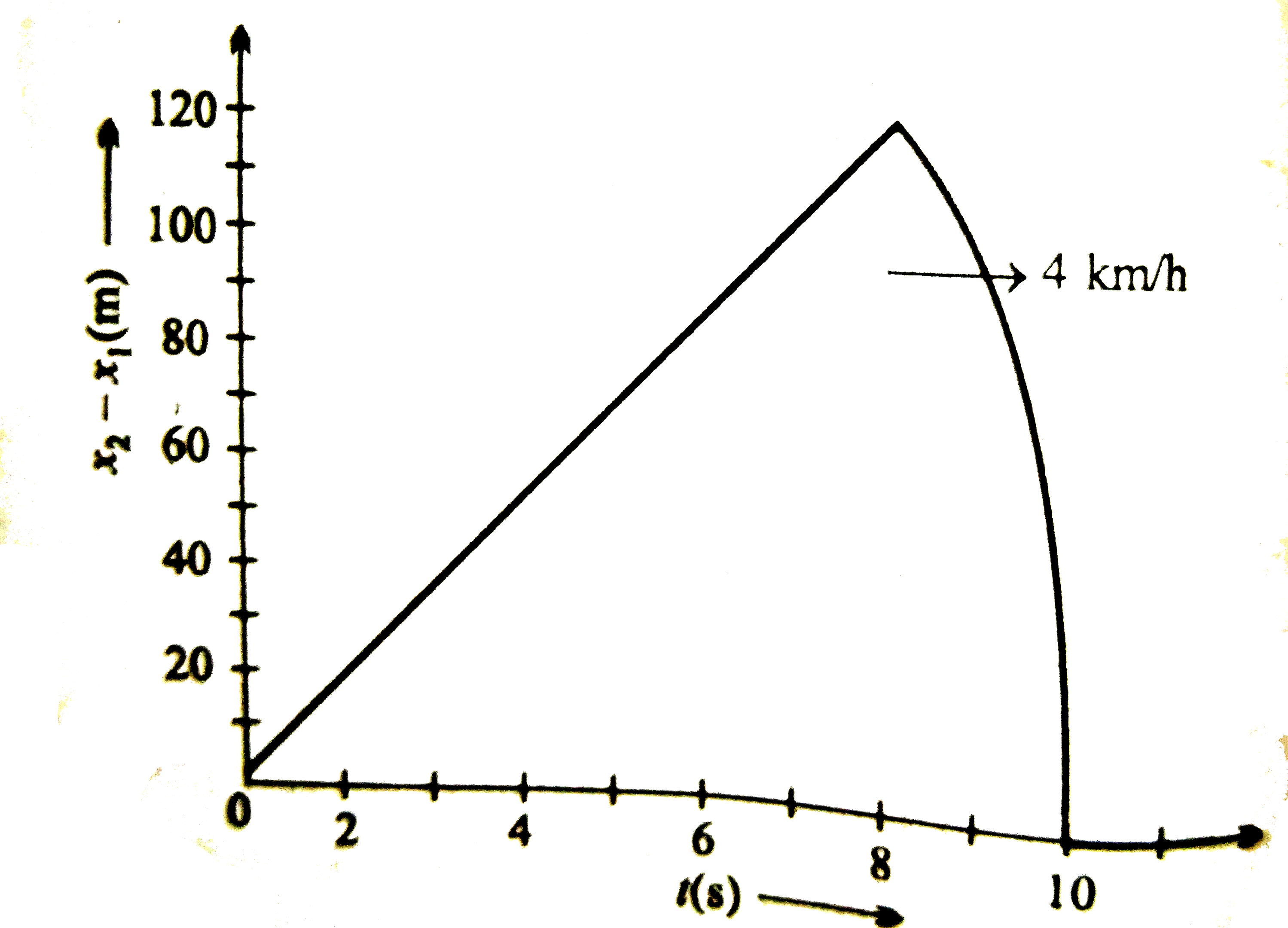
किसी 200 m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15ms−1 तथा 30ms−1 की प्रारंभिक चाल से फेंका जाता है । इसका सत्यापन कीजिए कि नीचे दिखाया गया ग्राफ ( चित्र ) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है । वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछाले नहीं । मान लीजिए g=10ms−2| ग्राफ के रेखीय व वक्रीय भागों के लिए । समीकरण लिखिए ।
पहले पत्थर के लिए -
x0=200m,u=15ms−1,g=10ms−2
समीकरण x=x0+ut−12gt2 से,
x1=200+15t−12×10t2
या x1=200+15t−5t2
जमीन से टकराने पर x1=0,
∴ 200+15t−5t2=0
या t2−3t−40=0
या t2−8t+5t−40=0
या t(t−8)+5(t−8)=0
या (t−8)(t+5)=0
∴ t−8=0 या t+5=0
अतः t=8s या t=−5s (जो कि अर्थहीन है।)
x0=200m,u=30ms−1
दूसरे पत्थर के लिए - अतः समीकरण x=x0+ut−12gt2 से,
x2=200+30t−12×10t2
या x2=200+30t−5t2
जमीन से टकराने पर x2=0
या t2−6t−40=0
या t2−10t+4t−40=0
या t(t−10)+4(t−10)=0
या (t−10)+(t+4)=0
∴t=10s या t=−4s (जो की अर्थहीन है।)
समी. (2 ) में समी. (1 ) को घटाने पर,
x2−x1=1t
t=8s पर दोनों पत्थरों के बीच अधिकतम दुरी
x2−x1=15×8=120m
पहले पत्थर के जमीन पर पहुँचने अर्थात t=8s तक x2−x1 और t के बीच खींचा गया ग्राफ एक सरल रेखा होगा।
स्पष्टतः रेखीय भाग का समीकरण x2−x1=15t होगा।
t=8s से t=10s तक पहला पत्थर जमीन पर रहेगा जबकि दूसरा पत्थर गतिशील रहेगा, जहाँ x2=200+30t−5t2
या x2−x1=200+30t−5t2
यह एक परवलय का समीकरण है।
अतः वक्रीय भाग का समीकरण x2−x1=200+30t−5t2 होगा।
Topper's Solved these Questions
Similar Questions
यदि एक वस्तु एक लकड़ी के ब्लॉक में 3 सेमी भेदन करने पर आधा वेग खो देती है तो रुकने के पहले वः कितना और भेदन करेगी -
View Solutionनिम्नलिखित भौतिक राशियों में से बतलाइए की कौन - सी सदिश है और कौन - सी अदिश -
आयतन , द्रव्यमान , चाल ,त्वरण , घनत्व , मोल संख्या , वेग , कोणीय आवृति , विस्थापन , कोणीय वेग |
View Solutionसात सुरों को यह गजब की विविधता के साथ प्रस्तुत करती है। (कर्मवाच्य)
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionएक एंजाइम उत्प्रेरित अभिक्रिया के लिए, ताप (T) के सापेक्ष अभिक्रिया की दर (r) को आलेखित किया गया है। निम्नलिखित में से कौन सा सही निरूपण है?
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionग्लूकोज के ताजा तैयार विलयन से समय के साथ प्रकाशिक घूर्णन में परिवर्तन को निम्न में जाना जाता है -
View Solutionगैस के दाब के साथ ठोस की सतह पर गैसों के अधिशोषण के लिए निम्नलिखित में से सही परिवर्तन है
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution1 M NaOH विलयन के 2.5 लीटर को अन्य 0.5 M NaOH विलयन के 3 लीटर के साथ मिलाया जाता है। परिणामी विलयन की मोलरता है -
View Solutionनिम्नलिखित में से कौनसा आरेख एक प्रबल विद्युत अपघट्य के लिए तनुकरण के साथ तुल्यांकी चालकत्व (A) की सही परिवर्तनशीलता को प्रदर्शित करता है?
View Solutionबेन्जैल्डिहाइड बनाने के लिए AlCl3 की उपस्थिति में बेन्जीन के साथ CO+HCI की अभिक्रिया को क्या कहा जाता है?
View SolutionNaOH की उपस्थिति में, फीनॉल के साथ बेंजॉयल क्लोराइड की अभिक्रिया को कहा जाता है:
View Solutionनिम्नलिखित में से कौनसा आरेख एक प्रबल विद्युत् अपघट्य के तनुकरण के साथ मोलर चालकत्व (Delta_m) के परिवर्तन को सही रूप से प्रदर्शित करता हैं?
View Solution

