A mass of 2.9 kg is suspended from a string of length 50 cm and is at rest. Another body of mass 100 g, which is moving horizontally with a velocity of 150m/s strikes and sticks to it. Subsequently when the string makes an angle of 60∘ with the vertical, the tension in the string is (g = 10m/s2)Solution in Telugu
140 N
135 N
125 N
90 N
The correct Answer is:B
From Law of conservation of momentum
m1+m2U2=m1V1+m2V2
2.9×0+0.1×150=(2.9+0.1)V
v=5m/s
For circular motion,
Centripetal force = Net force towards centre
⇒m1+m2v21l=T−(m1+m2)gcos60∘
⇒T=3×9.8×12+3v210.5
=14.7+6V21
According to Law of conservation of mechanical energy,
K.E at lowest point = (K.E + P.E)
12(m1+m2)V2=12(m1+m2)V_(1)(2)+(m1+m2)gh
(12)(3)(5)2=12(3)V21+3×9.8×0.5(1−12)
[∵h=l(1−cosθ)=0.5(1−cos60∘)]
V21=20.1(m/sec)
On substituting V2 in equation (1),
T=14.7+6×20.1=135.3N.

Topper's Solved these Questions
Similar Questions
R.M.S. velocity of oxygen molecules at N.T.P. is 0.5 Km/s. The R.M.S. velocity of he hydrogen molecule at N.T.P. is
View SolutionA circular loop and a square loop are formed from two wires of same length and cross section. Same current is passed through them. Then the ratio of their dipole moments is
View SolutionA mass of 2.9kg is suspended from a string of length 50cm and is at rest . Another body of mass 100gm which is moving horizontal with a velocity of 150m/s strikes it . After striking the two bodies combine together . Tension in the string , when it is at an angle of 60∘ with the velocity is : g=10m/s2
View SolutionA mass of 2.9 kg, is suspended from a string of length 50 cm, and is at rest. Another body of mass 100 gm moving horizontally with a velocity of 150 m/sec, strikes and sticks to it. What is the tension in the string when it makes an angle of 60º with the vertical
View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
View SolutionA mass of 2 kg tied to a string 1 m length is rotate in a verticle circle with a uniform speed of 4m/s. The tension in the string will be 52 N, when the mass is at (g=10m/s2)
View SolutionA mass of 5 kg is tied to a string of length 1.0 m is rotated in vertical circle with a uniform speed of 4m/s . The tension in the string will be 170 N when the mass is at (g=10m/s2)
View SolutionA mass of 5 kg is tied to a string of length 1.0 m and is rotated in vertical circle with a uniform speed of 4m//s . The tension in the string will be 130 N when the mass is at (g= 10 m//s^2 )
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)
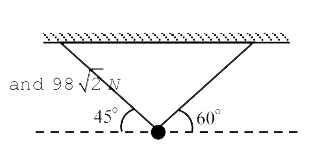
View SolutionA 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m//s^(2))
View SolutionA particle of mass 100 g is suspended from the end of a weightless string of length 100 cm and is rotated in a vertical plane. The speed of the particle is 200cm⋅s−1 when the string makes an angle of θ=60∘ with the verctcal. Determine
(i) the tension in the string when θ=60∘ and
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA mass of 3.9 kg suspended from a string of length 0.5 m is at rest. Another body of mass 0.1 kg moving horizontally with a velocity 200ms−1 strikes and stricks to it. The maximum angle through which the system swings just before the tension in the string becomes zero is
View SolutionA mass of 2.9 kg is suspended from a string of length 50 cm and is at rest. Another body of mass 100 g which is moving horizontally with any velocity of 150 m/s strikes and sticks to it subsequently when the string makes an angle of 60∘ with the vertical. The tension in the string is (g=10m/s2)
View SolutionA mass of 2.9 kg is suspended from a string of length 50 cm and is at rest. Another body of mass 100 g, which is moving horizontally with a velocity of 150m/s strikes and sticks to it. Subsequently when the string makes an angle of 60∘ with the vertical, the tension in the string is (g = 10m/s2)
View Solution

