Suppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E2)=12andP(E1∣E2)=14. Observe the lists given below :
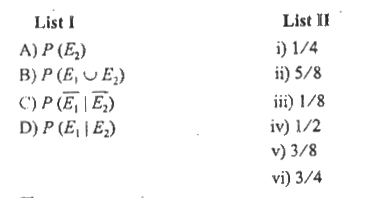
The correct matching of the list I from the list II is :Solution in Telugu
(A)(B)(C)(D)(a)(ii)(iii)(vi)(i)
(A)(B)(C)(D)(a)(iv)(v)(vi)(i)
(A)(B)(C)(D)(a)(iv)(ii)(vi)(i)
(A)(B)(C)(D)(a)(i)(ii)(iii)(i)
The correct Answer is:C
Step by step video, text & image solution for Suppose that E_1 and E_2 are two events of a random experiment such that P(E_(1))=1/4 , P(E_2 |E_2) =1/2 and P(E_1 |E_2)=1/4. Observe the lists given below : The correct matching of the list I from the list II is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
a(x)=∣∣ ∣ ∣∣123x+12x+13x+1x2+12x2+13x2+1∣∣ ∣ ∣∣⇒∫10A(x)dx=
View SolutionIf a unit vector is represented by 0.5ˆi+0.8ˆj+cˆk ,the value of c is
View SolutionStatement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1
View SolutionE1,E2 are events of a sample sapce such that P(E1) =1/4 , P(E2∣E1)=1/2,P(E1∣E2)=1/4. Then P(E1∣E2)+P(E1∣¯¯¯¯E2)=
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E2)=12andP(E1∣E2)=14. Observe the lists given below :
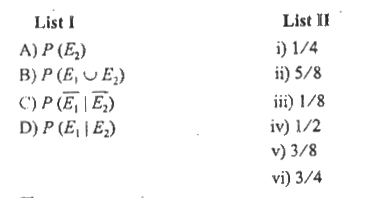
The correct matching of the list I from the list II is :
View SolutionSuppose E1 and E2 are two events of a sample space such that P(E1)=12,P(E2∣E1)=12,P(E1∣E2)=14 then P(E'2)= _____
View SolutionFill in the Blanks :
If E1 and E2 are independent events, then P(E1 ∩ E2) =..
View SolutionStatement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
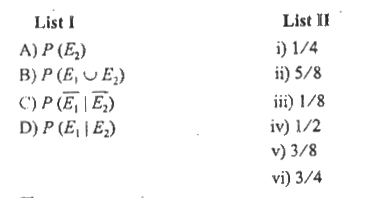
The correct matching of the list I from the list II is :
View SolutionIf E_1 and E_2 are two independent events associated with an experiment, then show that P(E_1cupE_2)=1-P(E_1^c)P(E_2^c)
View SolutionIf E1 and E2 are independent events associated with an experiment such that P(E1)=P1 and P(E2)=P2. Find
P(E1andE2).
View SolutionIf E_1 and E_2 are independent events associated with an experiment such that P(E_1)=P_1 and P(E_2)=P_2 . Find P(E_1 but not E_2) .
View SolutionIf E_1 and E_2 are independent events associated with an experiment such that P(E_1)=P_1 and P(E_2)=P_2 . Find P( neither E_1 nor E_2) .
View SolutionIf E1 and E2 are independent events associated with an experiment such that P(E1)=P1 and P(E2)=P2. Find
P(E1orE2).
View SolutionThere are two independent events E_1 and E_2 and P(E_1)=0.30 , P(E_2)=0.60 find the probability that both E_1 and E_2 occur.
View SolutionThere are two independent events E_1 and E_2 and P(E_1)=0.30 , P(E_2)=0.60 find the probability that neither E_1 nor E_2 occurs.
View Solution

