Consider a vessel filled with a liquid upto height H. The bottom of the vessel lies in the XY-plane passing through the origin. The density of the liquid varies with Z-axis as ρ(z)=ρ0[2−(zH)2]. If p1 and p2 are the pressures at the bottom surface and top surface of the liquid, the magnitude of (p1−p2) isSolution in Telugu
ρ0gH
85ρ0gH
32ρ0gH
53ρ0gH
The correct Answer is:D
Pressure at bottom
=g×∫z=Hz=01πr2×πr2×dz×ρ0(2−z2H2)
=g×∫z=Hz=0ρ0(2−z2H2)dz=g×[ρ(2z−z33H2)]z=Hz=0
=gρ0(2H−H33H2)=gρ0(2H−H3)
=gρ0(5H3)=53ρ0gh
Topper's Solved these Questions
Similar Questions
A force F is applied in a square plate of length L . If the percentage error in the determination of L is 3% and in F in 4% then permissible error in the calculation of pressure is
View SolutionA tokamak fusion test reactor works on
View SolutionCalculate the pressure inside a small air bubble of radus r situated at a depth h below the free surface of liquids of densities ρ1 and ρ2 and surface tennsions T1 and T2. The thickness of the first and second liquids are h1 and h2 respectively. Take atmosphere pressure =P0.

View Solution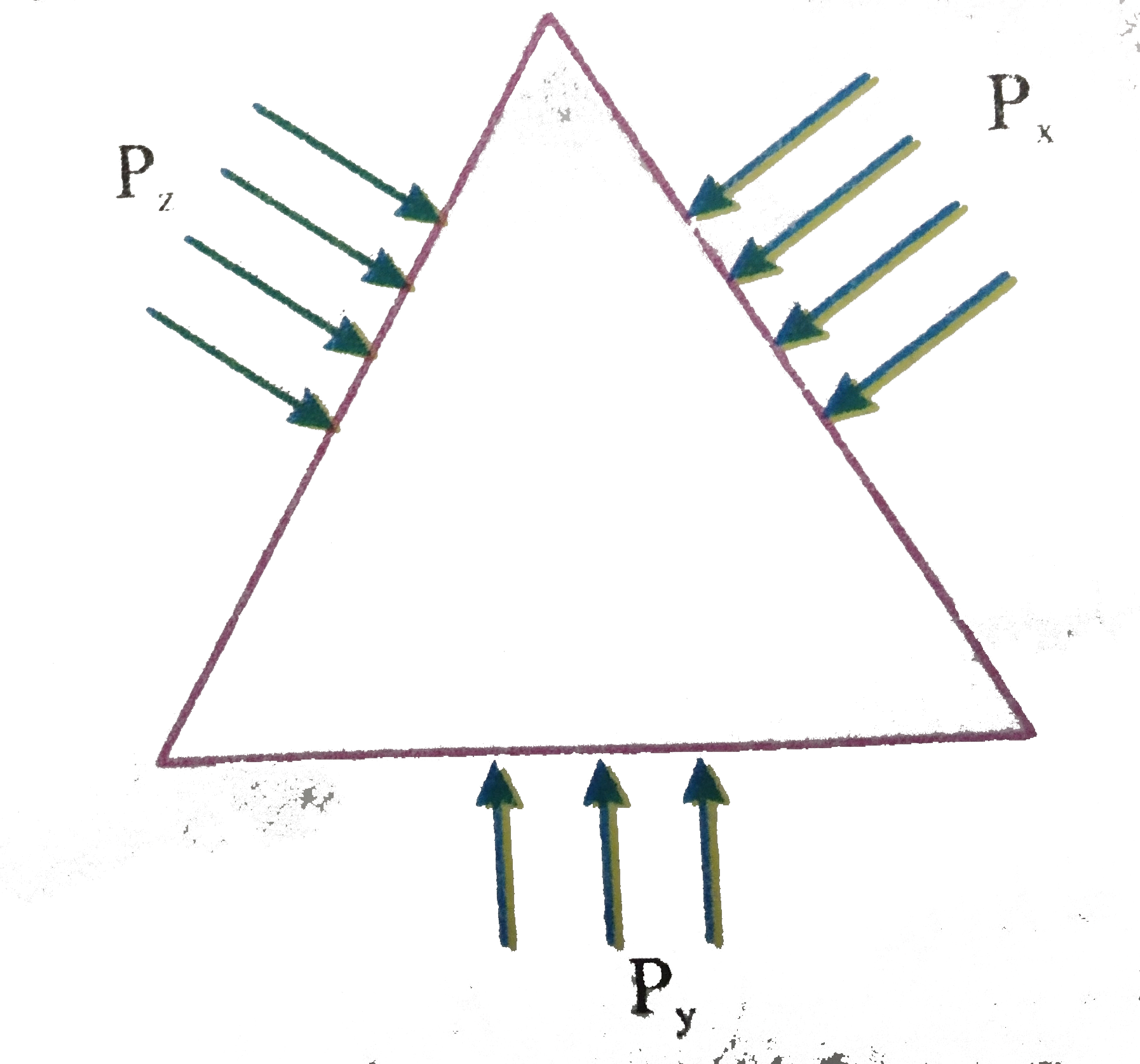
A triangular element of the liquid is shown in the fig. Px,Py and Pz represent the pressures on the element of the liquid then:
View SolutionA metal sphere connected by a string is dipped in a liquid of density rho as shown in figure. The pressure at the bottom of the vessel will be, (p_(0) =atmospheric pressure )
View SolutionThe top surface of an incompressible liquid is open to the atmosphere. The pressure at a depth h1 below the surface is p1 . What is the pressure p2 at depth h2=2h1 compare with p1 ?
View SolutionLet P1:2x+y+z+1=0
P2:2x−y+z+3=0 and P3:2x+3y+z+5=0 be three planes, then the distance of the line of intersection of planes P1=0 and P2=0 from the plane P3=0 is
View SolutionConsider a vessel filled with a liquid upto height H. The bottom of the vessel lies in the XY-plane passing through the origin. The density of the liquid varies with Z-axis as ρ(z)=ρ0[2−(zH)2]. If p1 and p2 are the pressures at the bottom surface and top surface of the liquid, the magnitude of (p1−p2) is
View SolutionA metal sphere connected by a string is dipped in a liquid of density rho as shown in figure. The pressure at the bottom of the vessel will be, (p_(0) =atmospheric pressure )
View SolutionCalculate the pressure inside a small air bubble of radus r situated at a depth h below the free surface of liquids of densities ρ1 and ρ2 and surface tennsions T1 and T2. The thickness of the first and second liquids are h1 and h2 respectively. Take atmosphere pressure =P0.

View SolutionThe pressure P1 at the top of a dam and P2 at a depth h from the top inside water (density ρ) are related as :
View SolutionLet P1:2x+y+z+1=0
P2:2x−y+z+3=0 and P3:2x+3y+z+5=0 be three planes, then the distance of the line of intersection of planes P1=0 and P2=0 from the plane P3=0 is
View SolutionA cylindrical vessel is filled with a liquid of density ρ to a height h such that the force exerted by the liquid on the bottom is equal to the force exerted on the walls of the vessel. Then h should be
View Solutionमाना की किसी पात्र में एक तरल विरामावस्था में है चित्र में बिंदु 1, बिंदु 2 से h ऊँचाई पर है बिन्दुओ पर दाब क्रमशः p1और p2 है
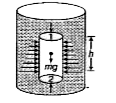
यदि बेलन में उपस्थित तरल का भार है mg तो यह तुल्य होगा (A=बेलन का क्षेत्रफल )
View Solutionमाना की किसी पात्र में एक तरल विरामावस्था में है चित्र में बिंदु 1, बिंदु 2 से h ऊँचाई पर है बिन्दुओ पर दाब क्रमशः p1और p2 है
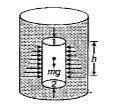
h गहराई पर दाब आधिक्य (p−p0)को कहते है
View Solution

