At t=0 and x=0 , an initially stationary blue car begins to accelerate at a constant rate of 2.0m/s2 in the positive direction of the x -axis At =t = 2s a red car travelling in an adjecent lane and in the same direction passes x =0 with a speed of 8.0m/s and a constant accleration of 3.0m/s2 .the time when red car passes the blue car is :
4.2 s
3.6 s
2.9 s
None of these
The correct Answer is:C
To solve the problem of when the red car passes the blue car, we will analyze the motion of both cars using the equations of motion.
1. Identify the motion parameters of both cars:
- Blue Car:
- Initial position, xB0=0
- Initial velocity, uB=0 (stationary)
- Acceleration, aB=2.0m/s2
- Time of motion, tB=t (we will find this time)
- Red Car:
- Initial position, xR0=0
- Initial velocity, uR=8.0m/s (starts at t=2s)
- Acceleration, aR=3.0m/s2
- Time of motion, tR=t−2 (since it starts moving 2 seconds later)
2. Write the equations of motion for both cars:
- Distance covered by the Blue Car:
xB=uBt+12aBt2=0+12(2)t2=t2
- Distance covered by the Red Car:
xR=uR(t−2)+12aR(t−2)2
Expanding this:
xR=8(t−2)+12(3)(t−2)2
xR=8t−16+32(t2−4t+4)=8t−16+32t2−6t+6
xR=32t2+2t−10
3. Set the distances equal to find when the cars meet:
xB=xR
t2=32t2+2t−10
4. Rearranging the equation:
t2−32t2−2t+10=0
−12t2−2t+10=0
Multiplying through by -2 to eliminate the fraction:
t2+4t−20=0
5. Use the quadratic formula to solve for t:
t=−b±√b2−4ac2a
Here, a=1,b=4,c=−20:
t=−4±√42−4⋅1⋅(−20)2⋅1
t=−4±√16+802
t=−4±√962
t=−4±4√62
t=−2±2√6
6. Select the positive root:
t=−2+2√6
Approximating √6≈2.45:
t≈−2+4.9≈2.9s
Conclusion:
The time when the red car passes the blue car is approximately t≈2.9s.
- Blue Car:
- Initial position, xB0=0
- Initial velocity, uB=0 (stationary)
- Acceleration, aB=2.0m/s2
- Time of motion, tB=t (we will find this time)
- Red Car:
- Initial position, xR0=0
- Initial velocity, uR=8.0m/s (starts at t=2s)
- Acceleration, aR=3.0m/s2
- Time of motion, tR=t−2 (since it starts moving 2 seconds later)
- Distance covered by the Blue Car:
xB=uBt+12aBt2=0+12(2)t2=t2
xR=uR(t−2)+12aR(t−2)2
Expanding this:
xR=8(t−2)+12(3)(t−2)2
xR=8t−16+32(t2−4t+4)=8t−16+32t2−6t+6
xR=32t2+2t−10
xB=xR
t2=32t2+2t−10
t2−32t2−2t+10=0
−12t2−2t+10=0
Multiplying through by -2 to eliminate the fraction:
t2+4t−20=0
t=−b±√b2−4ac2a
Here, a=1,b=4,c=−20:
t=−4±√42−4⋅1⋅(−20)2⋅1
t=−4±√16+802
t=−4±√962
t=−4±4√62
t=−2±2√6
t=−2+2√6
Approximating √6≈2.45:
t≈−2+4.9≈2.9s
The time when the red car passes the blue car is approximately t≈2.9s.
Similar Questions
A motorboat starting from rest on a lake acceleration line at a constant rate of 3.0m/s2 for 8.0s. How far does the boat travel during this time ?
View SolutionThere are two cars on a straight road, marked as x axis. Car A is travelling at a constant speed of VA=9m/s. Let the position of the Car A, at time t=0, be the origin. Another car B is L=40m ahead of car A at t=0 and starts moving at a constant acceleration of a=1m/s2 (at t = 0). Consider the length of the two cars to be negligible and treat them as point objects.
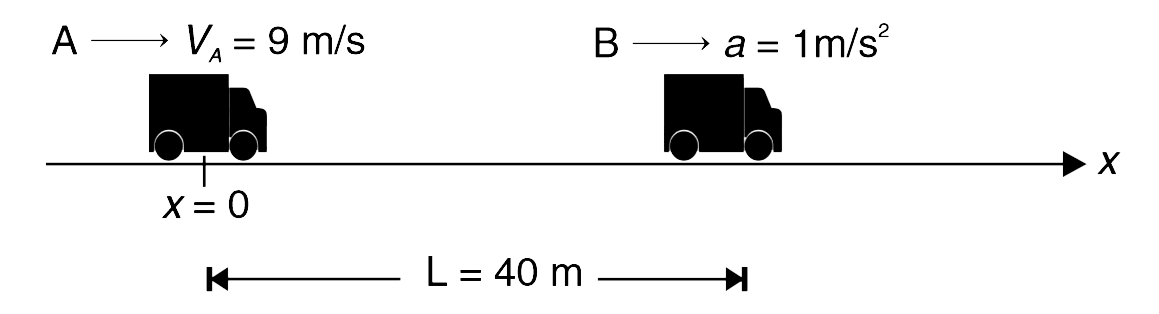
(a) Plot the position–time (x–t) graph for the two cars on the same graph. The two graphs intersect at two points. Draw conclusion from this.
(b) Determine the maximum lead that car A can have.
View Solution
Knowledge Check
A car travelling along a road begins accelerating with a constant acceleration of 1.5m/s2 in the direction of motion. After travelling 392 m at this acceleration, its speed is 35 m/s. Determine the speed of the car when it began accelerating.
A1.5 m/sB34 m/sC7.0 m/sD49 m/sA car accelerates from rest at a constant rate of 2m/s2 and comes to rest. If it remains in motion for 3 seconds, then the maximum speed attained by the car is :
A2 m/sB3 m/sC4 m/sD6 m/sTwo cars A and B are at rest at the origin O. If A starts with a uniform velocity of20m/s and B starts in the same direction with a constant acceleration of 2m/s2, then the cars will meet after time
A10sB20sC30sD40s
At time t=0 s a car passes a point with velocity of 16m/s and thereafter slows down with acceleration a=−0.5tm/s2 ,where t is in seconds. It stops at the instant t=
View SolutionA car is moving in a circular path of radius 500m with a speed of 30m/s. If the speed is increased at the rate of 2m/s2, the resultant acceleration will be .
View SolutionA train 100 m long completely passes a man walking in the same direction at 6 kmph in 5 s and a car travelling in the same direction in 6s. Find the speed of the car
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View SolutionA car is travelling at 20 m/s on a circular road of radius 100 m. It is increasing its speed at the rate of 3 m/s2. Its acceleration is
View Solution

