Three particles start from the origin at the same time, one with a velocity v1 along the x-axis, second along the negative y-axis with a velocity v2 and third particle moves along the line x = y. The velocity of third particle, so that three may always lie on the same line is:
v1v2v1+v2
√2v1v2v1+v2
√3v1v2v1+v2
zero
The correct Answer is:B
After time t, the particles reach A ,B ,& C
(##VMCPHYXIWORBOK01_C02E03005_S01.png width=80%><br> " " OA =V_1t<br>" " OB =v_2t <br> " "OC =V_3t<br> " "C∞rd∈ates:A ( v_1t.0) ,B( 0,v_2t) , C( (v_3)/(sqrt( 2)) t,(V_3)/(sqrt((2))t) <br>L∈eAB: (x)/( v_1t) +(y)/(v_2t) =1 " " Cshod––lieonAB,<br> (V_3)/(V_1sqrt2)+(V_3)/(v_2sqrt(2)=1 " "," " 1//v_3=((v_1+v_2)/(sqrt 2v_1v_2) " "," " v_3 =(sqrt( 2)v_1v_2)/(v_1+v_2)
Similar Questions
Three particles start from the origin at the same time, one with velocity u1 along the x-axis, the second with velocity u2 along the y-axis . Find the velocity of the third particles, along the x=y line so that the three particles may always lie on the same straight line.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View Solution
Knowledge Check
Three particles start from origin at the same time: one with velocity v1 along positive x-axis, the second along the positive y-axis with a velocity v2 and the third along the line y = x with such a speed that all the three always stay in a straight line, then velocity of the third particles is:
A√v1v2Bv1+v22Cv1v2√v21+v22Dv1v2√2v1+v2Three particles starts from origin at the same time with a velocity 2ms−1 along positive x-axis, the second with a velocity 6ms−1 along negative y-axis, Find the velocity of the third particle along x=y line so that the three particles may always lie in a straight line.
A−3√3B3√2C−3√2D2√2Three particles A,B and C start from the origin at the same time,A with a velocity a along x-axis, B with a velocity b along y-axis and C with velocity c in XY plane along the line x=y.The magnitude of c so that the three always remain collinear is:
Aa+b2B√abCaba+bD√2aba+b
A particle moves from A to B with a uniform velocity v1 and from B to A with a velocity v2. If it moves along a straight line between A and B, then the average velocity of the particle is
View SolutionAt any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
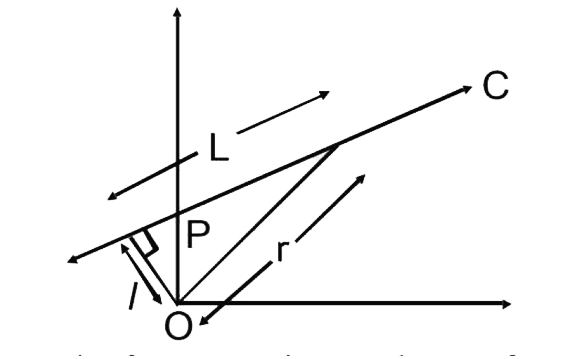
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View Solution

