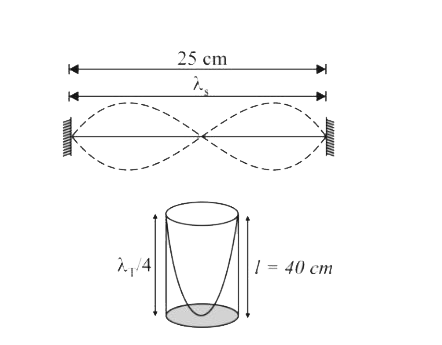
A string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/s, find the tension in the string.
The correct Answer is:27.04
For the first overtone of string
Linear mass density of the string= Mass of string per unit
Length =2.5×10−30.25=0.01kg/m
fs=1λ√Tm=10.25√T0.01…..(i)
Fundamenta frequency of closed organ
∴λT4=0.4⇒λT=1.6m,v=fTλT
fT=CλT=3201.6=200Hz.....(II)
In this case 8 beats/second is heard. The beat frequency decreases with the decreasing tension.This means that beat frequency decreass with decreasing fs. This mean that beat frequency is guven by the expression fbeat=fs−fT
∴8=10.25√T0.01−200⇒√T0.01=208×0.25=52⇒T=0.01×522=27.04N
Similar Questions
A string 25cm long fixed at both endds and having a mass of 2.5g is under tension. A pipe closed from one end is 40cm long. When the strin is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. If is observed that decreasing the tension in the string decreases the beat frequency. If the speed of sound in air is 320m/s. Find tension in the string.
View SolutionA string 1m long and having linear mass density 10g/m is sounded with a closed pipe of length 75cm. When string is vibrating in its first overtone and the air in the pipe in its fundamental frequency, 5beats/s are heard. It is observed that decreasing the tension in the string decreases the beat frequency. If the speed of sound in air is 315m/s, Find the tension in the string.
View Solution
Knowledge Check
A string of length 50cm and mass 12.5g is fixed at both ends. A pipe closed at one end has a length 85cm. When the string vibrates in its second overtone and the air column in the pipe in its first. Overtone, they produce a beats frquency of 6Hz. It is also observed that decreasing teh tension in the string decreaes beats frequency. Neglect the end correction in the pipe and velocity of sound in air is 340m/s. then the tension in the string is
A72NB52NC26ND18NIn law of tension, the fundamental frequency of vibrating string is
AInversely proportional of square root of tensionBDirectly proportional to the square root of tensionCDirectly proportional to the square of tensionDInversely proportional to densityA string 2.0 m long and fixed at its ends is driven by a 240 Hz vibrtor. The string vibrates in its third harmonic mode. The speed of the wave and its fundamental frequency is :
A320ms−1,120HzB180ms−1,80HzC180ms−1,120HzD32ms−1,80Hz
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension is the string is slightly increased . The original frequency of vibration of the string is
View SolutionA string 1 m long with mass 0.1 g cm−1 is under a tension of 400 N.Find is fundamental frequency of vibration.
View SolutionA tuning fork of frequency 512 Hz produces 6 beats per sec. with vibrating string of an instrument. On increasing the tension in the string, the beat frequency reduces to 3 beats/sec. Find the original frequency of the instrument.
View SolutionA hollow pipe of length 0.8m is closed at one end. At its open end a 0.5m long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is 50N and the speed of sound is 320ms−1, the mass of the string is
View SolutionA tuning fork of frequency 512 Hz is vibrated with sonometer wire and 6 beats per seconds are heard. The beat frequency reduces if the tension in the string is slightly increased. The original freqency of vibration of the string is
View Solution
