An open pipe of sufficient length is dipping in water with a speed v vertically. If at any instant l is lengths of tube avoce water. Then the rate at which fundamental frequency of pipe changes , is ( speed of sound = c)

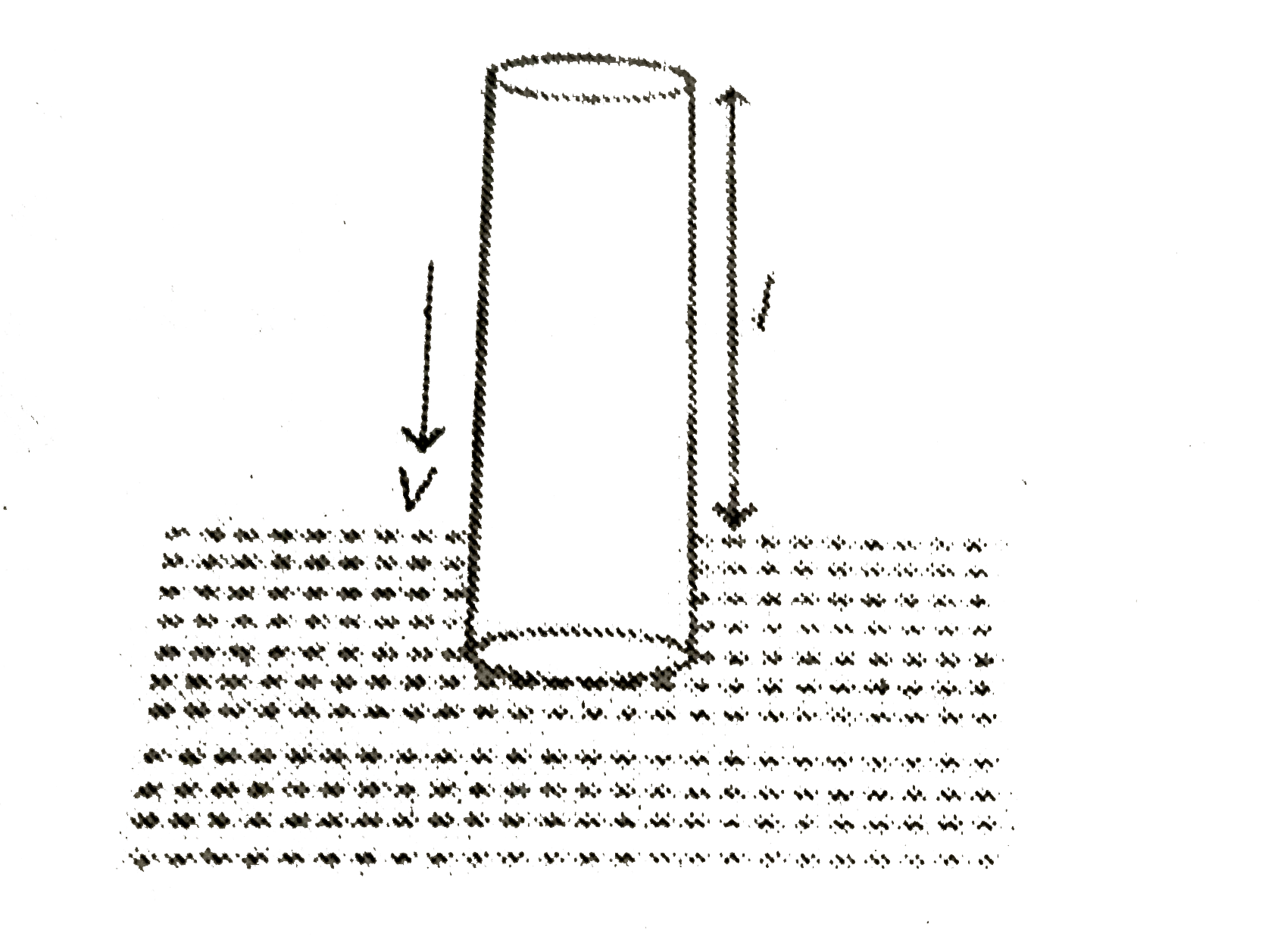
$c v / 2 I^{2}$

$c v / 4 I^{2}$

$c / 2 v^{2} I^{2}$

$c / 4 v^{2} I^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

An open pipe of sufficient length is dipping in water with a speed V vertically if at any instant l is length of tube above water then the rate at which fundamental frequency of pipe changes is (C is the speed of sound in air )

A $\frac{C V}{2} l^{2}$
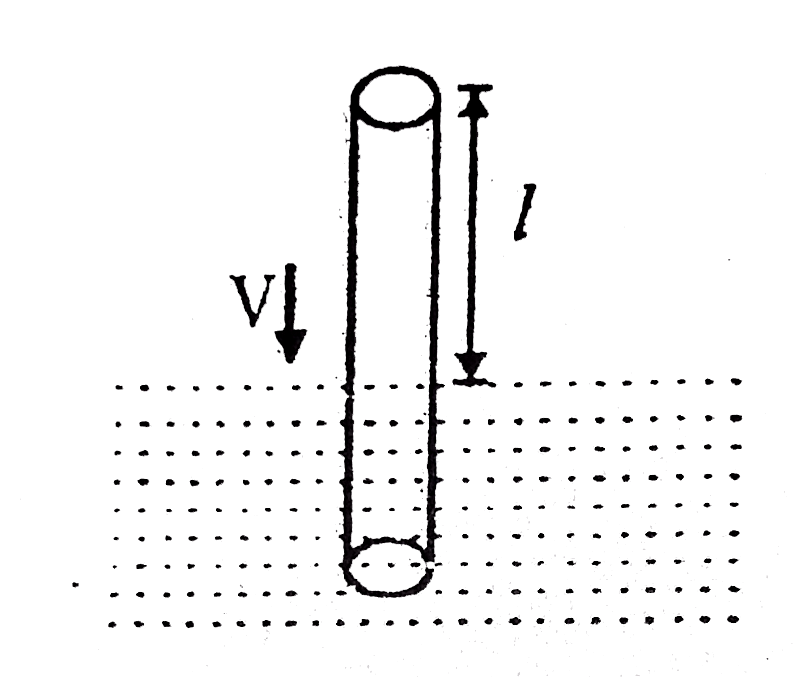B $\frac{C V}{4} l^{2}$
C $\frac{C V}{2 v^{2} t^{2}}$
D $\frac{C V}{4 v^{2} t^{2}}$
In an organ pipe of length L open at both ends, the fundamental mode has a frequency
(where v is a speed of sound in air)
A $\frac{v}{2 L}$ and only odd harmonies are present.
B $\frac{v}{2 L}$ and only even harmonies are present.
C $\frac{v}{2 L}$ and all harmonies are present.
D $\frac{v}{4 L}$ and only odd harmonies are present.
In an open end organ pipe of length $l$ if the speed of sound is $V$ then the fundamental frequency will be
A $\frac{V}{2 l}$ and both odd as well as even harmonics are present
B $\frac{V}{4 l}$ & both odd as well as even harmonics are present
C $\frac{V}{2 l}$ and only even harmonics are present
D $\frac{V}{4 l}$ and only even harmonics are present