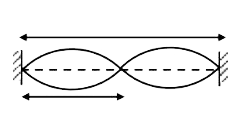
A string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 5 mm. The amplitude of a particle at distance l/8 from the fixed end is
5√2mm
5√2mm
5mm
10√2mm
The correct Answer is:A
A'=2Asinkx
For second, 2.λ2=l⇒λ=l
At x=l/8
A'=2Asin(2πλ⋅λ8)=2Asinπ4=2A((1√2)=5√2mm
Similar Questions
Knowledge Check
A string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 2 mm. The amplitude of a particle at distance l/8 from the fixed end is
A5√2mmB5√2mmC5mmD10√2mmA string of length l is fixed at both ends. It is vibrating in its 3rd overtone with maximum amplitude 'a'. The amplitude at a distance l/3 from one end is
AaB0C√3a2Da2A string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
AaB0C(√3a)2Da2
A string of length l is fixed at both ends. It is vibrating in its 3rd overtone with maximum amplitude a=2√3 mun. Find the square of amplitude (in (min)2 ) at a distance l/(3) from one end.
View SolutionA string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
View SolutionA string of length l along x-axis is fixed at both ends and is vibrating in second harmonic. If at t=0, y=2.5mm for incident wave, the equation of standing wave is (T is tension and μ is linear density)
View SolutionA string of length L between the two bridges of sonometer wire vibrates in the second harmonic. Its amplitude of vibration is maximum at
View SolutionA string of length 3L is fixed at both ends it resonates with a tunning fork in third harmonic with amplitude at antinode equal to A0 at time t=0 a string element at position of antinode is at half its positive amplitude and moving towards mean position displacement of a string element at L/2 is given by
View Solution
