A transverse sinusoidal wave of amplitude a, wavelength λ and frequency f is travelling on a stretched string. The maximum speed of any point in the string is v/10, where v is the speed of propagation of the wave. If a=10−3m and v=10ms−1, then λ and f are given by
2π×10−2m
10−3m
π×10−3m
2π×10−3m
The correct Answer is:A
Maximum speed of any point on the string aω=a(2πf)
∴=v10=1010=1 (givenv=10jm/s)
∴2πaf=1⇒f=12πa
a=10−3m (given)
∴f=12π×10−3=1032πHz
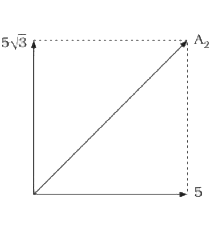
Speed of wavev=fλ ∴(10m/s)=(1032πs−1)λ
⇒∴λ=2π×10−2m
Similar Questions
A sinusoidal transverse wave of amplitude 10−2 m, wavelength λ, frequency f is travelling with speed (V = 20 m/s) on a stretched string. If the maximum speed at any point of the string is V5 then find the frequency and wavelength of the wave.
View SolutionA transverse wave of amplitude 2 m, wavelength 4 m and frequency 6 Hz is propagating in a string toward positive y-direction. The equation of the wave may be (y is in m and t is in s)
View Solution
Knowledge Check
A transverse sinusoidal wave of amplitude a, wavelength λ and frequency f is travelling on a stretched string. The maximum speed of any point in the string is v/10, where v is the speed of propagation if the wave. If a=10−3m and v=10ms−1, then lanbda and f are given by
A(a) λ=2π×10−2mB(b) λ=10−3mC( c ) f=103Hz/(2π)D(d) f=104HzA transverse sinusoidal wave of amplitude A, wavelength λ and frequency f is travelling along a stretch string. The maximum speed of any point on the string is v10, where, V is the velocity of wave propagation. If A=10−3m,andV=10ms−1, then λ and f are given by
Aλ=2π×10−2mBλ=10−2mCf=1032πHzDf=104HzSpeed (v), wavelength (λ) and the frequency (f) of sound are related as
Aλ=v×fBv=fλCf=vλDnone
A transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is
View SolutionA sine wave has an amplitude A and wavelength λ. Let V be the wave velocity and v be the maximum velocity of a particle in the medium. Then
View SolutionA sinusoidal transverse wave is traveling on a string. Any point on the string
View SolutionTwo identical sinusoidal waves each of amplitude 10 mm with a phase difference of 90∘ are travelling in the same direction in a string. The amplitude of the resultant wave is
View Solution