Question

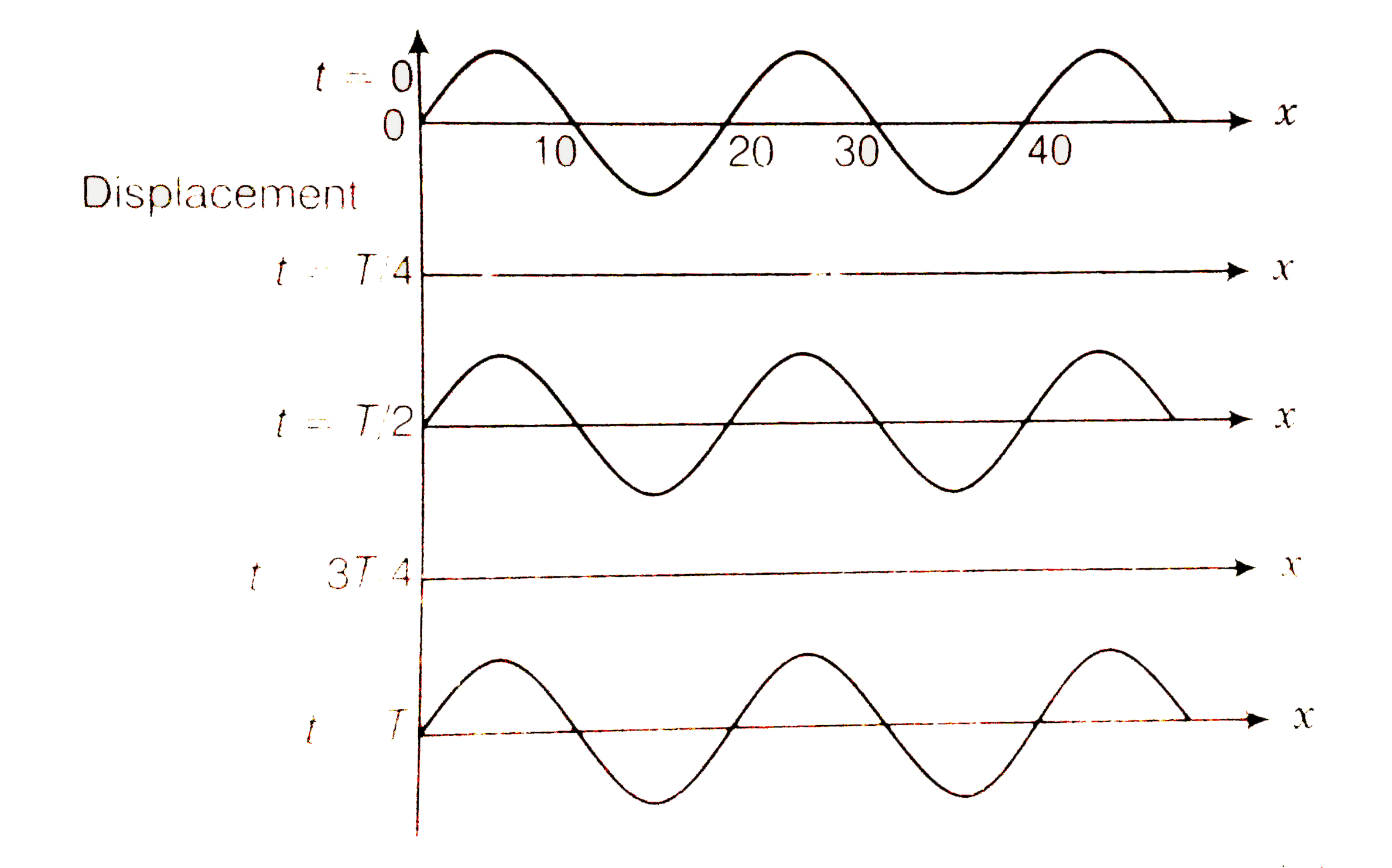
The pattern of standing waves formed on a stretched string at two in -stants of time are shown of time are shown in figure. The velocity of two waves superim-posing to form stationary waves is $360m{s}^{-1}$ and their frequencies are 256 Hz.

(a) Calculate the time at which the second curve is plotted.
(b) Mark nodes and antinodes on the curve.
(c) Calculate the distance between A' and C'

Explanation

(i) Here, `v=360ms^(-1),v=256Hz`
`lamda=(v)/(u)=(360)/(256)=1.406m`
`A A'=(lamda)/(4)=(1,406)/(4)=0.3516m`
Time (t) at which the second curve is plotted `(A A')/(v)=(0.3516)/(360)=9.8xx10^(-4)s`
(ii) Nodes A,B,C,D,E, antinodes A',C'
(iii) Distance between A' and C', `lamda=1.406m=1.41m`.