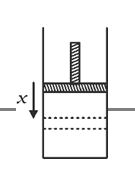
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass $M$ . The piston and the cylinder have equal cross - section area $A$ . When the piston is in equilibrium, the volume of the gas is $(V_{0})$ and the its pressure is $(P_{0})$ . The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, Show that the piston executes simple harmonic motion and find the frequency of oscillations.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{1}{2} π \sqrt{γ \frac{p_{0} A^{2} + M g A}{V_{0}} M}$

$(\frac{1}{2 π} \sqrt{\frac{γ (p_{0} A^{2} + M g A)}{V_{0} M}})$
In equilibrium pressure inside the cylinder = pressure just outside it
or $P = P_{0} + \frac{M g}{A}$
When piston is displaced slightly by an amount x, change in volume,
Since, the cylinder is isolated from the surroundings, process is adiabatic in nature. In adiabatic process,
$\frac{d P}{d V} = - γ \frac{P}{V}$
or increase in pressure inside the cylinder, $d p = - \frac{(γ P)}{V} (d V) = γ ⎛ ⎜ ⎝ \frac{P_{0} + \frac{M g}{A}}{V_{0}} ⎞ ⎟ ⎠ (A x)$
This increase in pressure when multiplied with area of cross-section A will give a net upward force (or the restoring force). Hence,
$F = - (d P) A = - γ (\frac{P_{0} A^{2} + M g A}{V_{0}}) x$ or $a = \frac{F}{M} = - γ (\frac{P_{0} A^{2} + M g A}{V_{0} M}) x$
Since, $a \propto - x$ motion of the piston is simple harmonic in nature. Frequency of this oscillation is given by
$f = \frac{1}{2 π} \sqrt{∣ ∣ \frac{a}{x} ∣ ∣} = \frac{1}{2 π} \sqrt{\frac{γ (P_{0} A^{2} + M g A)}{V_{0} M}}$

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile