For a particle executing SHM, the displacement x is given by x=Acosωt. Identify the graph which represents the variation of potential energy (PE) as a function of time t and displacement x.

(a) I,III
(b) II,IV (c ) II,III
(d) I,IV
I, III
II, IV
II, III
I, IV
The correct Answer is:A
We know that in SHM, at extreme position, PE is maximum when t=0, x=A, i.e., at time t=0, the oarticle executing SHM is at its extreme position. Therefore, PE is maximum. Graphs-I and III represent the above characteristics.
Similar Questions
For a particle executing simple harmonic motion, the displacement x is given by x=Acosωt. Identify the graph, which represents the variation of potential energy (U) as a function of time t and displacement x.

View SolutionIf for a particle executing SHM, the equation of SHM is given as y=acosωt. Then which of the following graphs represents the variation in potential energy?
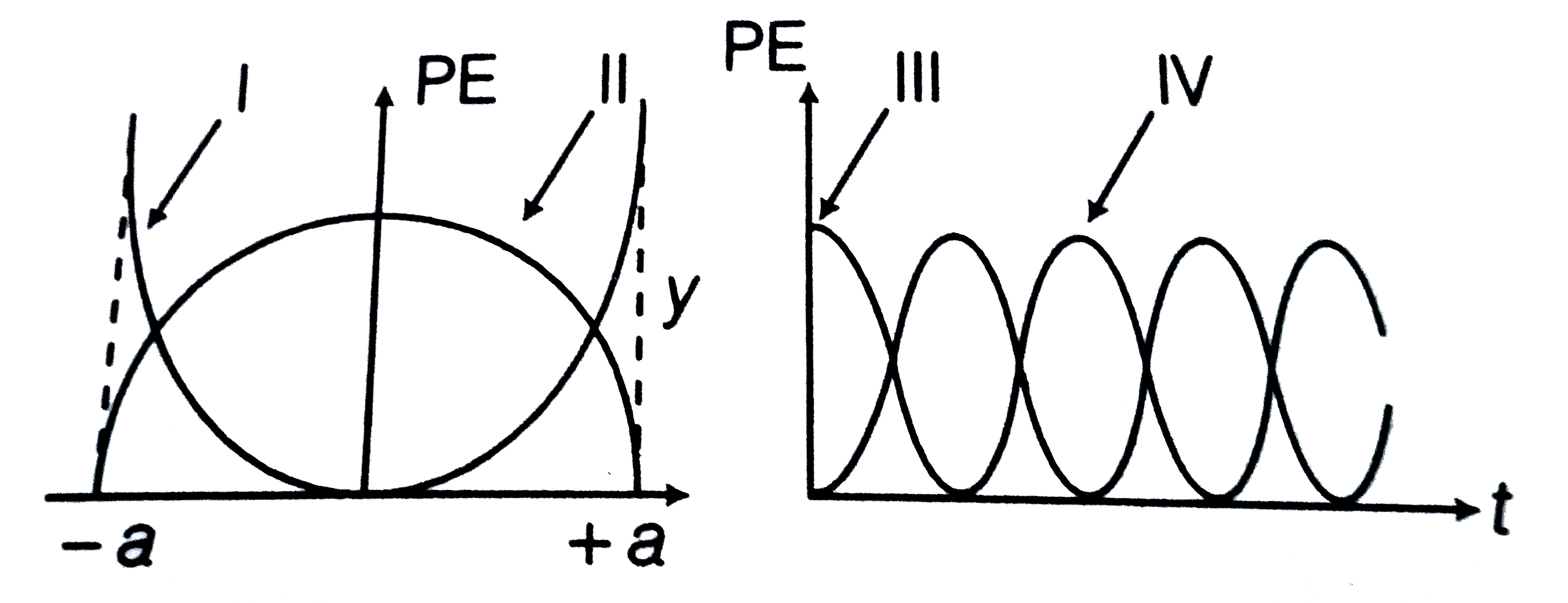
View Solution
Knowledge Check
For a particle executing S.H.M. the displacement x is given by x=Acosωt . Identify the graph which represents the variation of potential energy (P.E.) as a function of time
 AI,IIIBII, IVCII, IIIDI,IV
AI,IIIBII, IVCII, IIIDI,IVFor a particle executing SHM, the kinetic energy (K) is given by K=K0cos2ωt. The equation for its displacement is
A(K0mω2)12sinωtB(2K0mω2)12sinωtC(2ω2mK0)12sinωtD(2K0mω2)12sinωtThe displacement of a particle is given by x=cos2ωt. The motion is
Asimple harmonicBperiodic but not simple harmonicCperiodic but not simple harmonicDNone of the above
Which of the following graphs best represents the variation of acceleration 'a' with displacement x?
View SolutionThe displacement of a particle executing a S.H.M. is given by x= A "sin" ωt+Acosωt. What is the amplitude of motion ?
View SolutionThe potential energy of a particle (Ux) executing SHM is given by
View SolutionAssertion : x-t equation of a particle in SHM is given as :x=Acosωt
Reason : In the given equation the minimum potential energy is zero.
View SolutionA particle is executing S.H.M. along a straight line. The graph showing the variation of kinetic, potential and total energy K, U and T respectively with displacement is -

View Solution
