Consider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
At a distance x1 from the equilibrium position, kinetic energy of the oscillating system becomes equal to potential energy then, x1is equal to:
Q The minimum value of coefficient of friction such that the cylinder does not slip on the surface is:
mgK
KAmg
32KAmg
KA3mg
The correct Answer is:D
fmax=kA3⇒μmg=kA3∴μ=kA3mg
Similar Questions
A small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
View SolutionA solid cylinder of mass 'm' is attached to a horizontal spring with a force constant K. The cylinder can roll without slipping along the horizontal plane as shown in the figure. Find the time period of centre of mass of the cylinder
View SolutionA solid cylinder (see figure) connected to a horizontal massless spring can accelerate without slipping along the horizontal surface. When the spring is drawn 0.3 m, this body is released from the break at t = 0. The period of oscillation of the cylinder's mass center will be
View SolutionA solid cylinder of mass m is attached to a horizontal spring with force constant k . The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T = 2pisqrt((3m)/(2k)) , if displaced from mean position.
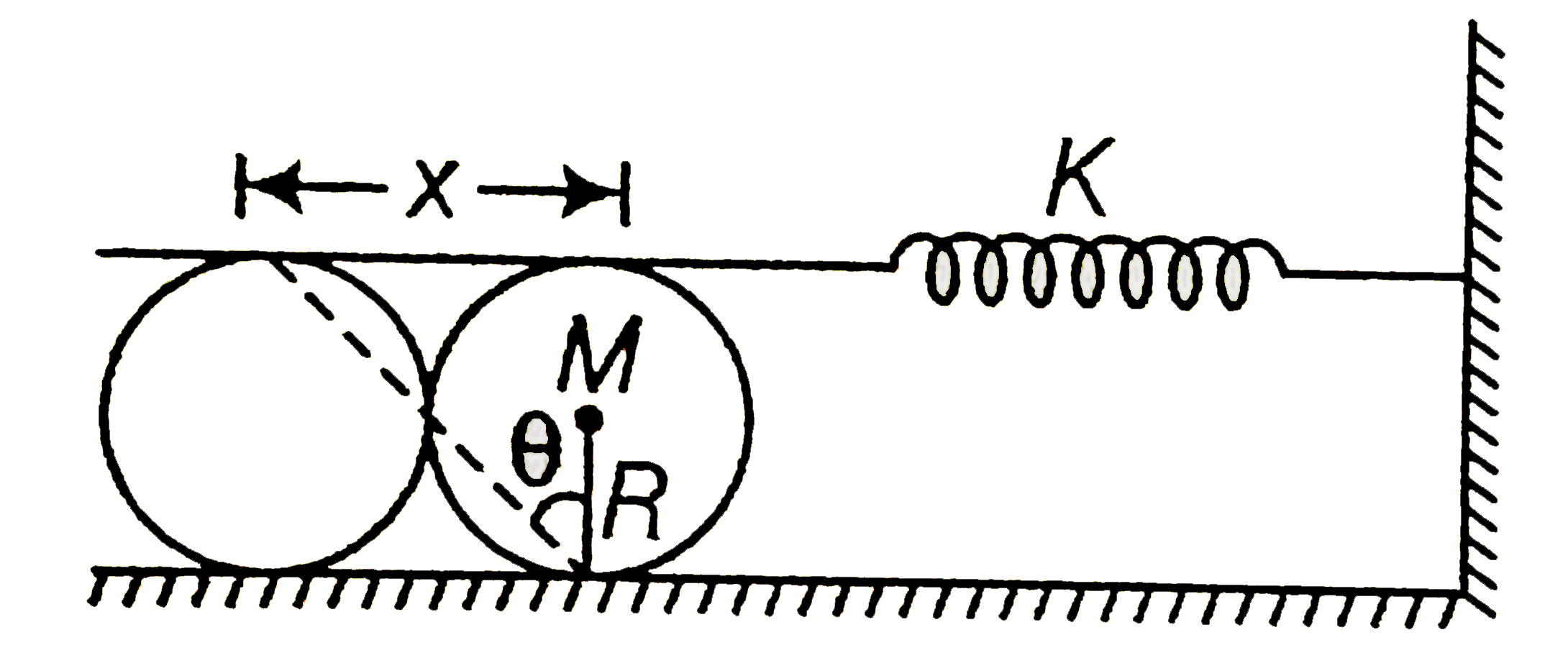
View SolutionA uniform cylinder of mass M and radius R rolls without slipping down a slope of angle 8 with horizontal. The cylinder is connected to a spring of force constant k at the centre, the other side of which is connected to a fixed support at A. The cylinder is released when the spring is unstretched. The· force of friction (f) :
View SolutionA solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
At a distance x1 from the equilibrium position, kinetic energy of the oscillating system becomes equal to potential energy then, x1is equal to:
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.

:
Q The minimum value of coefficient of friction such that the cylinder does not slip on the surface is:
View Solution

