A U-tube of uniform cross-section holds 1 kg of pure mercury and 0.2 kg of water in equilibrium. The diameter of cross-section is 1.2 cm. Relative density of mercury is 13.6. If the system in equilibrium is slightly disturbed, the period of oscillation of the liquid column in the tube will be (takeg=10ms−2)
1.0 s
1.54 s
1.50 s
2.0 s
The correct Answer is:B
To solve the problem, we need to determine the period of oscillation of the liquid column in a U-tube containing mercury and water. Let's break it down step by step.
Step 1: Understand the System
We have a U-tube with:
- 1 kg of mercury
- 0.2 kg of water
- The diameter of the cross-section is 1.2 cm.
Step 2: Calculate the Cross-sectional Area
The radius r of the U-tube is:
r=1.2cm2=0.6cm=0.006m
The cross-sectional area A is given by:
A=πr2=π(0.006)2≈1.131×10−7m2
Step 3: Determine the Effective Mass
The total mass of the liquid column is the sum of the masses of mercury and water:
M=1kg+0.2kg=1.2kg
Step 4: Calculate the Density of Mercury
The relative density of mercury is given as 13.6. Therefore, the density ρm of mercury is:
ρm=13.6×1000kg/m3=13600kg/m3
Step 5: Calculate the Restoring Force
When the liquid column is displaced by a distance x, the restoring force Fr can be expressed as:
Fr=Pressure×A=h⋅ρ⋅g⋅A
where h=2x (the height difference created by the displacement), ρ is the density of the liquid, and g is the acceleration due to gravity.
Step 6: Substitute Values
The restoring force can be expressed as:
Fr=2x⋅ρm⋅g⋅A
Substituting the values:
Fr=2x⋅13600⋅10⋅1.131×10−7
Step 7: Relate to Simple Harmonic Motion
For SHM, the restoring force is also given by:
Fr=−kx
where k is the force constant. From the above equation, we can equate:
k=2⋅13600⋅10⋅1.131×10−7
Step 8: Calculate the Angular Frequency
The angular frequency ω is given by:
ω=√kM=√2⋅13600⋅10⋅1.131×10−71.2
Step 9: Calculate the Period of Oscillation
The period T of oscillation is given by:
T=2πω
Substituting the expression for ω:
T=2π√Mk
Step 10: Final Calculation
Now we can plug in the values and calculate T:
T=2π√1.22⋅13600⋅10⋅1.131×10−7
Calculating this gives us:
T≈1.54seconds
Final Answer
The period of oscillation of the liquid column in the U-tube is approximately 1.54 seconds.
---
We have a U-tube with:
- 1 kg of mercury
- 0.2 kg of water
- The diameter of the cross-section is 1.2 cm.
The radius r of the U-tube is:
r=1.2cm2=0.6cm=0.006m
The cross-sectional area A is given by:
A=πr2=π(0.006)2≈1.131×10−7m2
The total mass of the liquid column is the sum of the masses of mercury and water:
M=1kg+0.2kg=1.2kg
The relative density of mercury is given as 13.6. Therefore, the density ρm of mercury is:
ρm=13.6×1000kg/m3=13600kg/m3
When the liquid column is displaced by a distance x, the restoring force Fr can be expressed as:
Fr=Pressure×A=h⋅ρ⋅g⋅A
where h=2x (the height difference created by the displacement), ρ is the density of the liquid, and g is the acceleration due to gravity.
The restoring force can be expressed as:
Fr=2x⋅ρm⋅g⋅A
Substituting the values:
Fr=2x⋅13600⋅10⋅1.131×10−7
For SHM, the restoring force is also given by:
Fr=−kx
where k is the force constant. From the above equation, we can equate:
k=2⋅13600⋅10⋅1.131×10−7
The angular frequency ω is given by:
ω=√kM=√2⋅13600⋅10⋅1.131×10−71.2
The period T of oscillation is given by:
T=2πω
Substituting the expression for ω:
T=2π√Mk
Now we can plug in the values and calculate T:
T=2π√1.22⋅13600⋅10⋅1.131×10−7
T≈1.54seconds
The period of oscillation of the liquid column in the U-tube is approximately 1.54 seconds.
Similar Questions
A thread of mercury of 10.2 g is in a tube of uniform cross-section 0.1cm2. Calculate the length of the thread. The density of mercury is 13.6gcm3.
View SolutionAn open U -tube of uniform cross-section contains mercury. When 27.2 cm of water is poured into one limb of the tube, (a) how high does the mercury rise in the limb from its initial level ? (b) what is the difference in levels of liquids of the two sides ? (ρw=1 and ρHg=13.6 units)
View Solution
Knowledge Check
In a vertical U - tube a column of mercury oscillates simple harmonically. If the tube contains 1kg of mercury and 1cm of mercury column weight's is 20g, then the period of oscillation is
A1sB2sC√2sDInsufficient dataThe cylienderical tube of a spray pump has a cross-section of 6cm2 one of which has 50 holes each of diameter 1 mm. If the liquid flow inside the tube is 1.2 m per minutes, then the speed of ejection of the liquid through the holes is
A2.1ms−1B0.31ms−1C0.96ms−1D3.4ms−1If cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
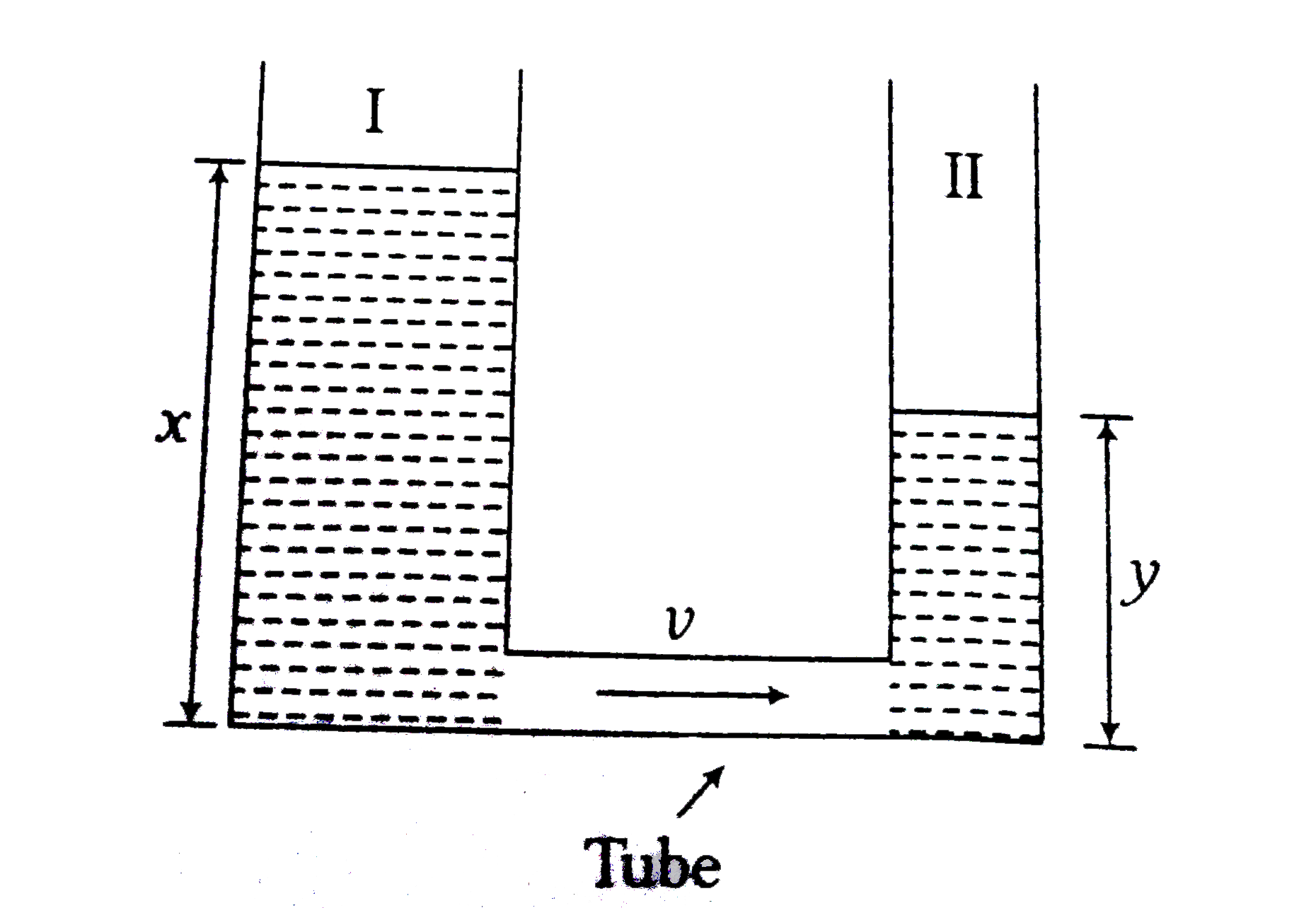 A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of these
A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of these
The cylindrical tube of a spray pump has a cross-section of 6 cm2 one of which has 50 holes each of diameter 1 mm. If the liquid flow inside the tube is 1.2 m/min, then speed of ejection of the liquid through the holes is
View SolutionA U - tube of uniform cross section contains mercury upto a height h in either limb. The mercury in one limbe is depressed a little and then relased. Obtain an expression for time period (T) of oscillation, assuming that T depends on h,ρ and g, where ρ is density of mercury.
View SolutionA wide vessel of uniform cross-section with a small hole in the bottom is filled with "40cm thick layer of water and "30cm" thick layer of kerosene.The relative density of kerosene is "],[0.8" .The initial velocity of flow of water streaming out of the hole is (take g=10ms−2
View SolutionA wide vessel of uniform cross- section with a small hole in the bottom is filled with 40cm thick layer of water and 30cm thick layer of kerosene.The relative density of kerosene is 0.8 .The initial velocity of flow of water streaming out of the hole is (take g=10ms−2 )
View SolutionThe area of cross section of the wider tube shown in figure is 900cm2. If the boy standing on the piston weights 45 kg, find the difference in the levels of water in the two tubes.

View Solution

