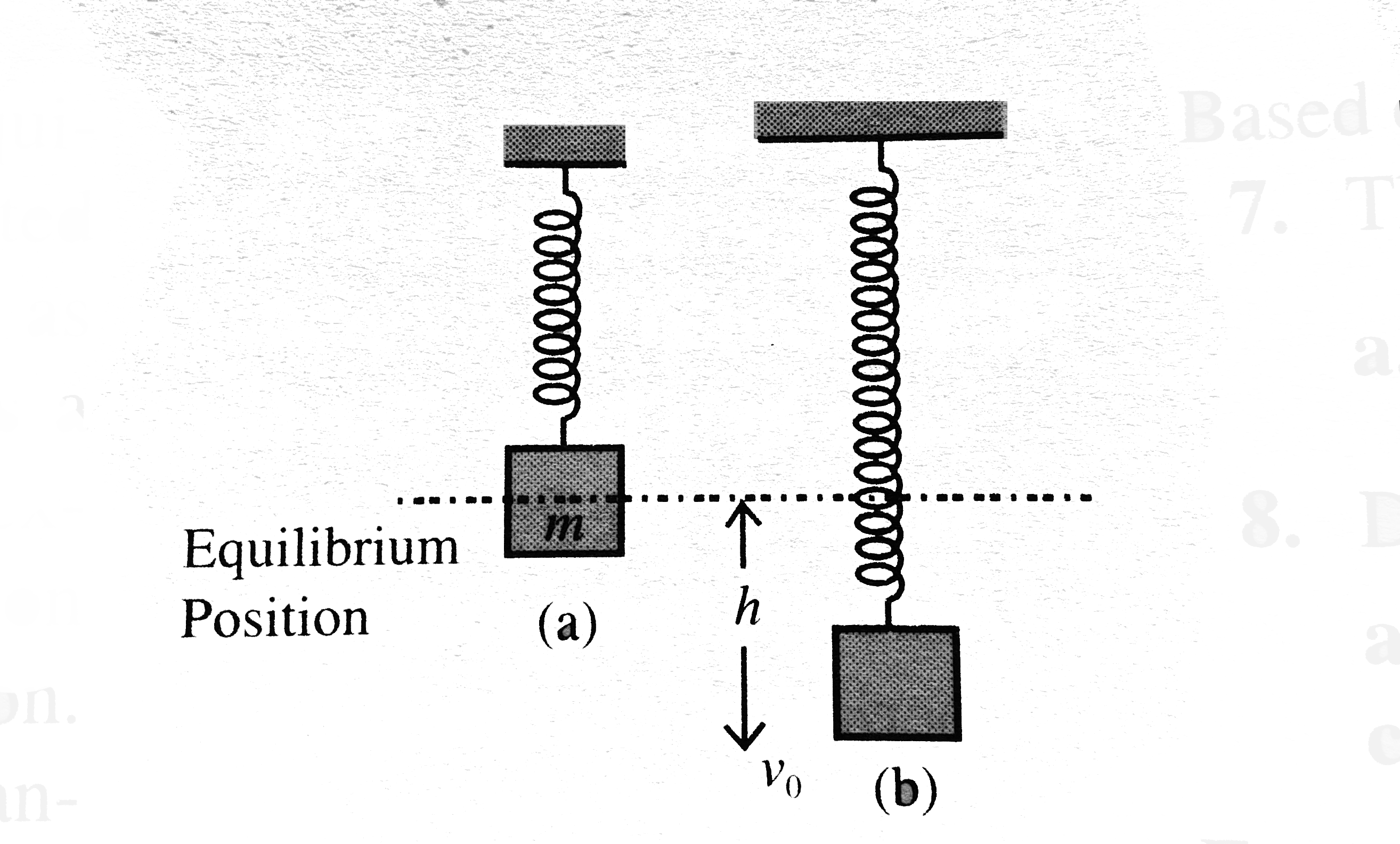
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed $v_{0}$ towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The equation for the simple harmonic motion is

$y = - A sin [\sqrt{\frac{k}{m}} t + {sin}^{- 1} (\frac{h}{A})]$

$y = - A cos [\sqrt{\frac{k}{m}} t + {sin}^{- 1} (\frac{h}{A})]$

$y = - A sin [\sqrt{\frac{k}{m}} t + {cos}^{- 1} (\frac{h}{A}) + \frac{π}{2}]$

$y = - A sin [\sqrt{\frac{k}{m}} t + {cos}^{- 1} (\frac{h}{A}) + \frac{π}{4}]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

To have the equilibrium of simple harmonic motion, it is best to represent simple harmonic motion as uniform circular motion. At t=0 let particle is making an angle $Σ$ with negative x-axis as shown, then
$sin Σ = \frac{h}{A} \Rightarrow Σ = {sin}^{- 1} (\frac{h}{A})$
At time t, $y = - A sin (ω t + Σ)$
So the equation of simple harmonic motion is $y = - \sqrt{\frac{m v_{0}^{2}}{k} + h^{2}} {sin [\sqrt{\frac{k}{m}} t + {sin}^{- 1} (\frac{h}{A})]}$

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Knowledge Check

Question 1 - Select One

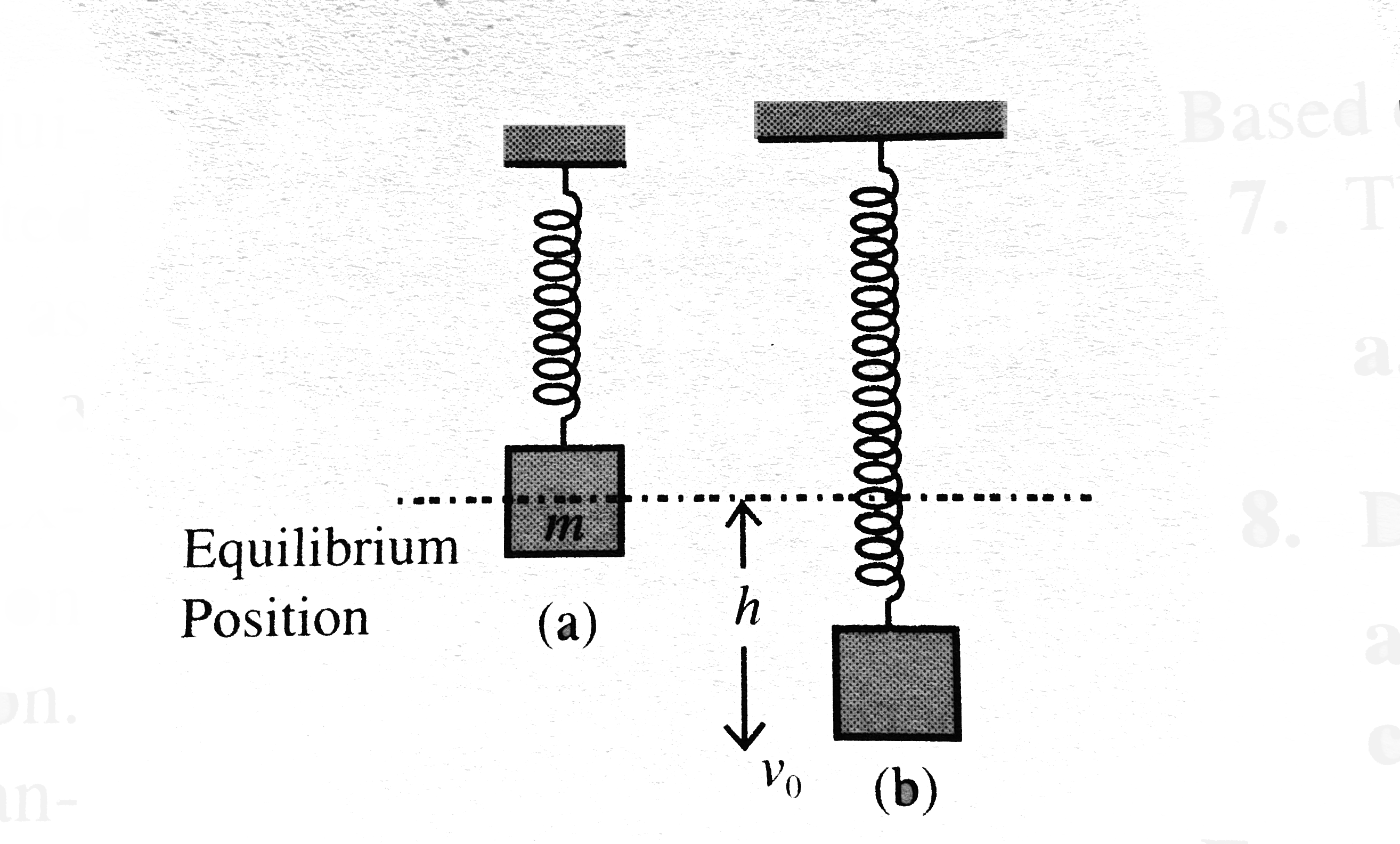
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed $v_{0}$ towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The amplitude of oscillation is
Ah
B $\sqrt{\frac{m v_{0}^{2}}{k} + h^{2}}$
C $\sqrt{\frac{m}{k} v_{0}} + h$
Dnone of these
Question 2 - Select One

A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed $v_{0}$ towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. Find the time taken by the block to cross the mean position for the first time.
A $\frac{2 π - {cos}^{- 1} (\frac{h}{A})}{\sqrt{\frac{k}{m}}}$
B $\frac{\frac{π}{2} - {cos}^{- 1} (\frac{h}{A})}{\sqrt{\frac{k}{m}}}$
C $\frac{π - {sin}^{- 1} (\frac{h}{A})}{\sqrt{\frac{k}{m}}}$
D $\frac{π - {sin}^{- 1} (\frac{h}{A})}{2 \sqrt{\frac{k}{m}}}$
Question 3 - Select One
A block of mass $m$ length force a verical of spring constant $k$ If the block is polled down by a distance of $2 m g / k$ from its equilibrium position and released for the subsequent in the spring to maximum compressed in it $m g / k$
A2
B3
C4
D1