Two particles are performing SHM in same phase. It means that
the two particles must have same distance from the mean position simultaneously
two particles may have same distance from the mean position simultaneously
the two particles must have maximum speed simultaneously
the two particles may have maximum speed simultaneously
The correct Answer is:BC
Y1=Asin(wt+ϕ1)
y−(2)=A1sin(w't+ϕ1=w't+ϕ2
if ϕTotal is same it means wt+ϕ1=w't+ϕ2 Same phase means the particle are at their mean position simultaneously. Also, they are at their extreme positions simultaneously . For this to happen, their Frequencies must also be equal . But their amplitudes can be different.
Similar Questions
Two particles are performing SHM with same amplitude and time period. At an instant two particles are having velocity 1m/s but one is on the right and the other is on left of their mean positiion. When the particles have same position there speed is √3m/s. Find the maximum speed (in m/s) of particles during SHM.
View SolutionThe position time graph for two particles- 1 and 2- performing SHM along X axis has been shown in the fig.
(a) Write the velocity of the two particles as a function of time.
(b) If the energy of SHM for the two particles is same write the ratio of their masses.
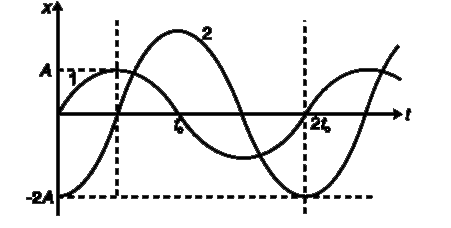
View Solution
Knowledge Check
For a particle performing SHM
AThe kinetic energy is never equal to the potential energyBthe kinetic energy is always equal to the potential energyCThe average kinetic in one time period is equal to the average potential in this periodDThe avarage kinetic energy in any time interval is equal to average potential energy in that interval.If the two particles performing S.H.M. with same amplitude and initial phase angle, then the initial phase angle of resultant motion depends on
Ainitial phase angle onlyBinitial phase angle and amplitude of individualCamplitudeof individual onlyDneither amplitude nor initial phase angleIf the two particles performs S.H.M. of same initial phase angle but different amplitudes of individuals, then the resultant motion initial phase angle depends on
Ainitial phase angle onlyBinitial phase angle and amplitude of individualCamplitude of individual onlyDneither amplitude nor initial phase angle
When two particles performing SHM of same amplitude and frequency arriving at a point of medium simultaneously with phase difference of π/2, then the resultant path is
View SolutionTwo particle are in SHM on same striaght line with amplitude A and 2A and with same angular frequency ω. It is observed that when first particle is at as distance A√2 from origin and going toward mean position, other particle is at extreme postion on other side of mean positon. find phase difference betwenen he two paricles.
View SolutionThe two particles performing S.H.M. have a phase difference of π. If the amplitude of second particle is three times the amplitude of first particle, then the amplitude of resultant motion will be
View SolutionDisplacement time graph of particle performing SHM is as shown in figure. Assume that mean position is at x=0
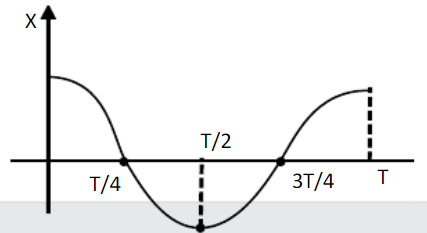
View SolutionAt two particular closest instant of time t1 and t2 the displacements of a particle performing SHM are equal. At these instant
View Solution
