An ice-cube of edge is 10 cm floating in water. Time period of small vertical oscillations of the cube is: (Specific gravity of ice is 0.9)
0.6s
1.6s
2.4s
3.6s
The correct Answer is:A
To solve the problem of finding the time period of small vertical oscillations of an ice cube floating in water, we can follow these steps:
1. Identify the Given Values:
- Edge length of the ice cube, a=10cm=0.1m
- Specific gravity of ice, SG=0.9
2. Convert Specific Gravity to Density:
- The specific gravity is defined as the ratio of the density of the object to the density of the fluid (water in this case).
- Let σ be the density of ice and ρ be the density of water.
- Since the specific gravity of ice is given as 0.9, we can express this as:
SG=σρ⟹σ=0.9ρ
- The density of water at 4∘C is approximately 1000kg/m3, hence:
σ=0.9×1000=900kg/m3
3. Determine the Height of the Ice Cube:
- The height of the ice cube h is equal to its edge length:
h=0.1m
4. Use the Formula for Time Period of Vertical Oscillation:
- The formula for the time period T of small oscillations of a floating object is given by:
T=2π√σhρg
- Substituting the values we have:
- σ=900kg/m3
- h=0.1m
- ρ=1000kg/m3
- g≈10m/s2
5. Calculate the Time Period:
- Plugging in the values:
T=2π√900×0.11000×10
- Simplifying the expression:
T=2π√9010000=2π√0.009=2π×0.09487
- Calculating the numerical value:
T≈2π×0.09487≈0.596s
- Rounding to one decimal place gives:
T≈0.6s
Final Answer:
The time period of small vertical oscillations of the ice cube is approximately 0.6 seconds.
- Edge length of the ice cube, a=10cm=0.1m
- Specific gravity of ice, SG=0.9
- The specific gravity is defined as the ratio of the density of the object to the density of the fluid (water in this case).
- Let σ be the density of ice and ρ be the density of water.
- Since the specific gravity of ice is given as 0.9, we can express this as:
SG=σρ⟹σ=0.9ρ
- The density of water at 4∘C is approximately 1000kg/m3, hence:
σ=0.9×1000=900kg/m3
- The height of the ice cube h is equal to its edge length:
h=0.1m
- The formula for the time period T of small oscillations of a floating object is given by:
T=2π√σhρg
- Substituting the values we have:
- σ=900kg/m3
- h=0.1m
- ρ=1000kg/m3
- g≈10m/s2
- Plugging in the values:
T=2π√900×0.11000×10
- Simplifying the expression:
T=2π√9010000=2π√0.009=2π×0.09487
- Calculating the numerical value:
T≈2π×0.09487≈0.596s
- Rounding to one decimal place gives:
T≈0.6s
The time period of small vertical oscillations of the ice cube is approximately 0.6 seconds.
Similar Questions
A solid cube floats in water half immersed and h small vertical oscillations of time period π5s. Find the mass (in kg) (Take g=10m/s2.
View SolutionAn ice cube of side 1cm is floating at the interface of kerosene and water in a beaker of base area 10cm2. The level of kerosene is just covering the top surface of the ice cube.
a. Find the depth of submergence in the kerosene and that in the water.
b. Find the change in the total level of the liquid when the whole ice melts into water.

View Solution
Knowledge Check
A block of ice of total area A and thickness 0.5m is floating in water. In order to just support a man of mass 100kg, the area A should be (the specific gravity of ice is 0.9)
A2.2m2B1.0m2C0.02m2DNone of theseA cube of ice of side length 10 cm is floating in water of density 1000 kg/m3. Then pick up the correct statement (density of ice = 900 kg/m3)
A1 cm of the cube will be out of waterB9 cm of the cube will be out of waterC9 cm of the cube will be in waterD1 cm of the cube will be in waterIceberg floats in sea water with a part of it submerged. The percentage fraction of the ice berg submerged is (density of ice = 0.9gcm−3, density of sea water = 1.1gcm−3)
A18%B12%C10%D8%
An ice cube floats in water. What percentage of volume is outside water. Density of water =1g/cc, density of ice =0.9g/cc.
View SolutionTwo ice cubes of side 10cm, having cavity of volume 20cm3 at centre of cube but filled with different materials A and B respectively. The specific gravity of material B is 1.9 Now these cubes are placed in two different vessels of same base area as shown in figure. The water level before putting blocks in vessels are same Assume that ice melts uniformly from all sides and with same constant rate in both the vessels. (specific gravity of ice=0.9)
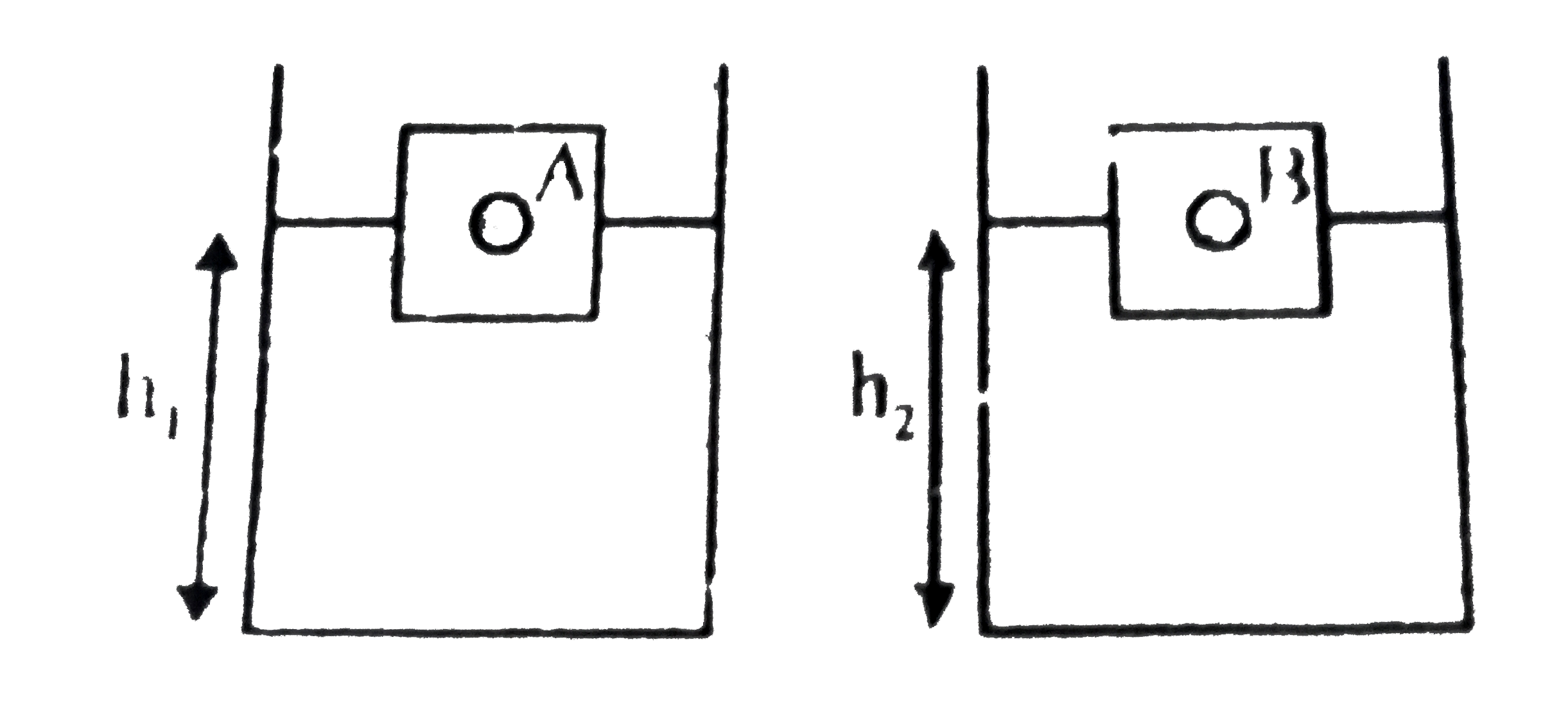 Choose the correct statement:
Choose the correct statement:
View SolutionAn ice cube is floating in a glass of water. What happens to the water level when the ice melts?
View SolutionTwo ice cubes of side 10cm, having cavity of volume 20cm3 at centre of cube but filled with different materials A and B respectively. The specific gravity of material B is 1.9 Now these cubes are placed in two different vessels of same base area as shown in figure. The water level before putting blocks in vessels are same Assume that ice melts uniformly from all sides and with same constant rate in both the vessels. (specific gravity of ice=0.9)
 Choose the correct graph showing the variation of heights of water- level in two vessels with time
Choose the correct graph showing the variation of heights of water- level in two vessels with time
View SolutionTwo ice cubes of side 10cm, having cavity of volume 20cm3 at centre of cube but filled with different materials A and B respectively. The specific gravity of material B is 1.9 Now these cubes are placed in two different vessels of same base area as shown in figure. The water level before putting blocks in vessels are same Assume that ice melts uniformly from all sides and with same constant rate in both the vessels. (specific gravity of ice=0.9)
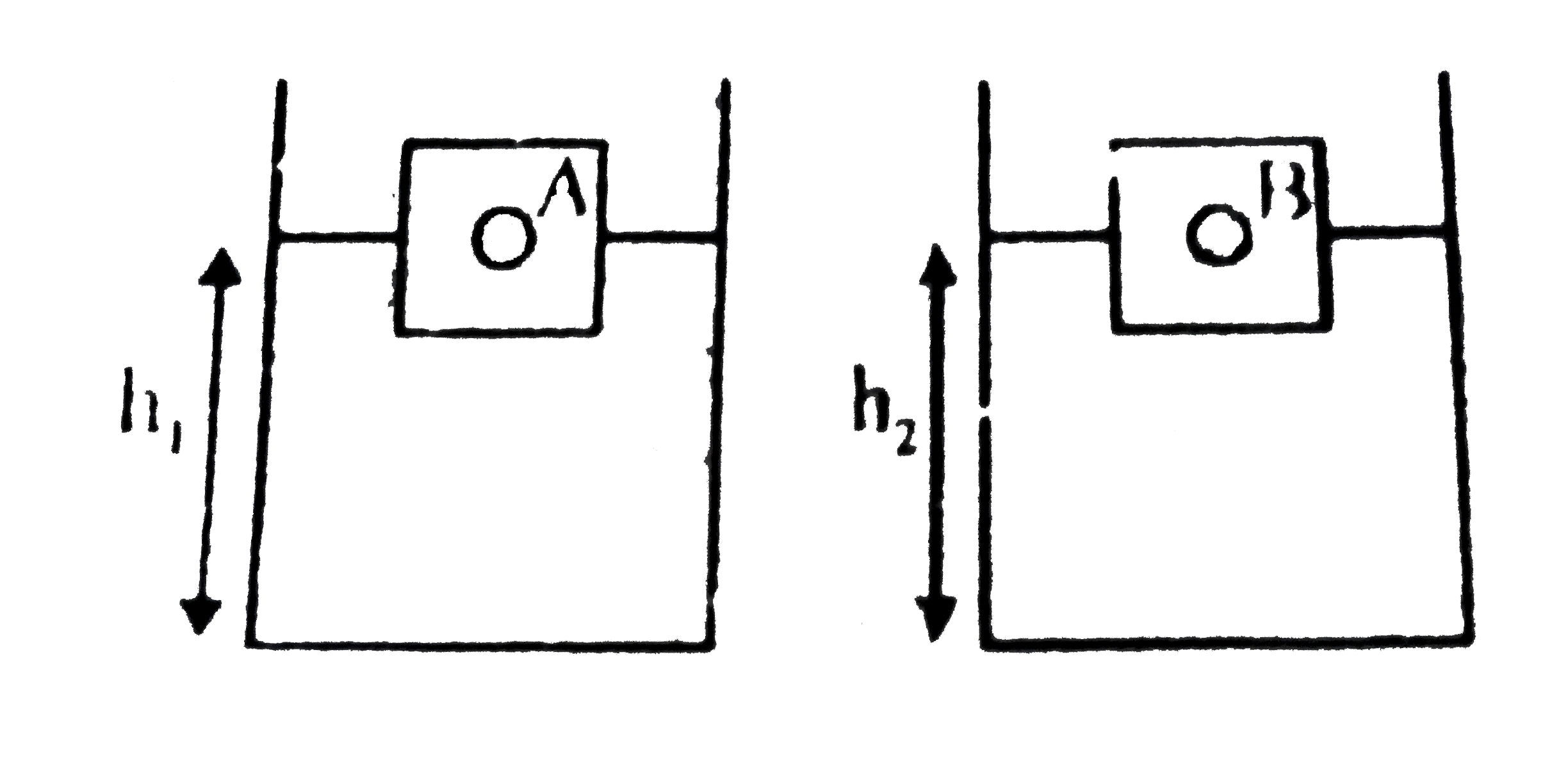 Find the ratio of initial submerged volumes of the blocks containing A and B respectively
Find the ratio of initial submerged volumes of the blocks containing A and B respectively
View Solution
