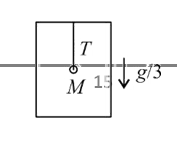
The time period of a simple pendulum of length L as measured in an elevator descending with acceleration g / 3 is

$2 π \sqrt{\frac{3 L}{g}}$

$π \sqrt{(\frac{3 L}{g})}$

$2 π \sqrt{(\frac{3 L}{2 g})}$

$2 π \sqrt{(\frac{3 L}{3 g})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Time period of simple pendulum is
A $T = 2 π \sqrt{\frac{l}{g}}$
B $T = 2 π \sqrt{\frac{g}{l}}$
C $T = \sqrt{2 π \frac{l}{g}}$
D $T = \frac{1}{2 π} \sqrt{\frac{g}{l}}$
The time period of a simple pendulum of infinte length is
Ainfinite
B $2 π \sqrt{R / g}$
C $2 π \sqrt{g / R}$
D $\frac{1}{2 π} \sqrt{R / g}$
The time period of a simple pendulum inside a stationary lift is T. If it starts descending with acceleration g/5. the new period of the simple pendulum will be
A2T
B $\frac{\sqrt{5}}{2} T$
C $\sqrt{\frac{5}{3}} T$
D $\frac{2}{\sqrt{5}} T$