A pendulum has a period for small osillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.

T
The correct Answer is:D
and Rightarrow Required time =
Similar Questions
The distance between the point of suspension of the pendulum and the bottom of the bob is the length of a simple pendulum
View SolutionA pendulum bob 'm' is released from rest from horizontal position as shown in the figure. ltbr> Choose the position where the chance of. Braking of the string is maximum.
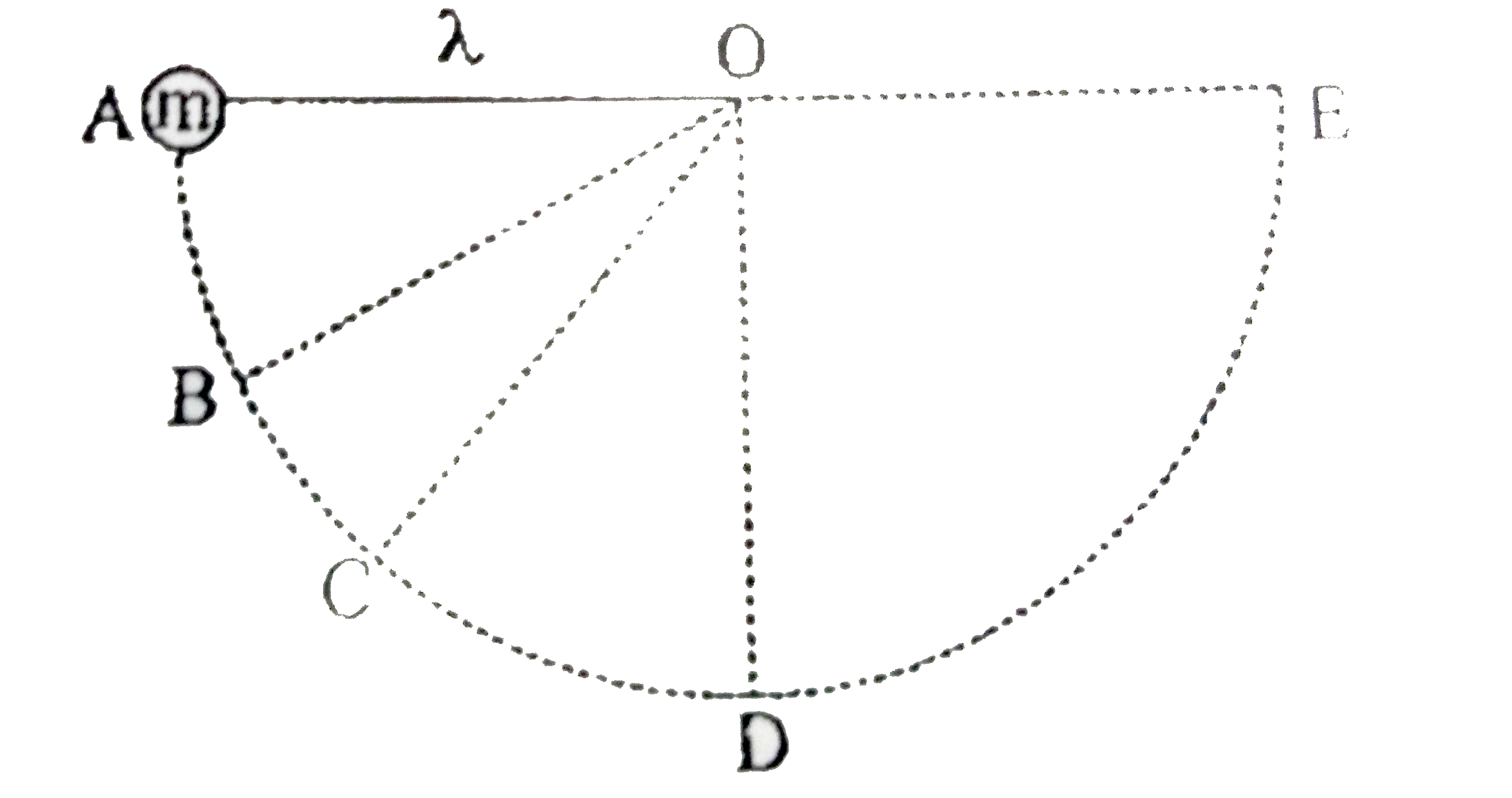
View Solution
Knowledge Check
A pendulum of length L swings from rest to rest n times in one second. The value of acceleration due to gravity is
A4π2n2LB2π2n2LCπ2n2LDπ2n2L2A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
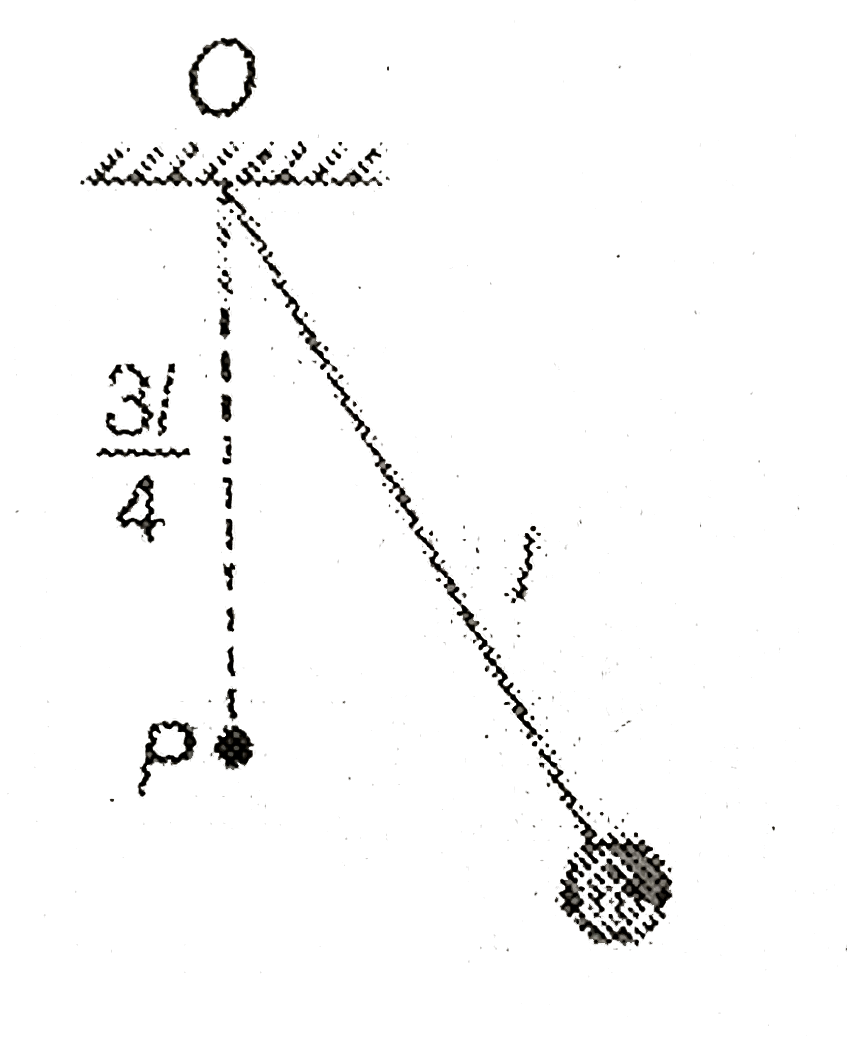 ATB3T4C3T5D4T5
ATB3T4C3T5D4T5A simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
 A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
The tension in the string of a simple pendulum is maximum, when the bob of the pendulum
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionIf the string of a pendulum were cut when the bob is at its central position, the bob would fall to the earth due to the absence of the
View SolutionIn a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
View SolutionA swinging pendulum has its maximum acceleration at
View Solution
