One mole of an ideal gas undergoes a process T = 300 + 2V. Then amount of work done by gas when volume increases from 2m3 to 4m3:
300RIn2+4R
2 + 2 In 2
300 R In 2
None of these
The correct Answer is:A
To solve the problem of calculating the work done by one mole of an ideal gas during the process where the temperature varies with volume as T=300+2V, we can follow these steps:
Step 1: Understand the Work Done by the Gas
The work done W by the gas during a volume change is given by the integral of pressure with respect to volume:
W=∫V2V1PdV
where V1=2m3 and V2=4m3.
Step 2: Use the Ideal Gas Law
According to the ideal gas law, we have:
PV=nRT
For one mole of gas (n=1), this simplifies to:
P=RTV
Substituting the expression for temperature T=300+2V:
P=R(300+2V)V=300RV+2R
Step 3: Set Up the Integral for Work Done
Now, substituting the expression for pressure into the work integral:
W=∫42(300RV+2R)dV
Step 4: Break Down the Integral
We can split the integral into two parts:
W=∫42300RVdV+∫422RdV
Step 5: Calculate Each Integral
1. First Integral:
∫42300RVdV=300R(lnV)42=300R(ln4−ln2)=300Rln(42)=300Rln2
2. Second Integral:
∫422RdV=2R(V)42=2R(4−2)=4R
Step 6: Combine the Results
Now, combining both parts of the integral:
W=300Rln2+4R
Final Result
Thus, the total work done by the gas when the volume increases from 2m3 to 4m3 is:
W=300Rln2+4R
The work done W by the gas during a volume change is given by the integral of pressure with respect to volume:
W=∫V2V1PdV
where V1=2m3 and V2=4m3.
According to the ideal gas law, we have:
PV=nRT
For one mole of gas (n=1), this simplifies to:
P=RTV
Substituting the expression for temperature T=300+2V:
P=R(300+2V)V=300RV+2R
Now, substituting the expression for pressure into the work integral:
W=∫42(300RV+2R)dV
We can split the integral into two parts:
W=∫42300RVdV+∫422RdV
1. First Integral:
∫42300RVdV=300R(lnV)42=300R(ln4−ln2)=300Rln(42)=300Rln2
∫422RdV=2R(V)42=2R(4−2)=4R
Now, combining both parts of the integral:
W=300Rln2+4R
Thus, the total work done by the gas when the volume increases from 2m3 to 4m3 is:
W=300Rln2+4R
Similar Questions
Knowledge Check
One mole of an ideal gas whose adiabatic exponent is γ=43 undergoes a process P=200+1V . Then change in internal energy of gas when volume changes from 2m2 to 4m3 is:
A400JB800JC1200JDNone of theseOne mole of ideal gas goes through processP=2V21+V2. Then change in temperature of gas when volume changes from V=1m2 to 2m2 is :
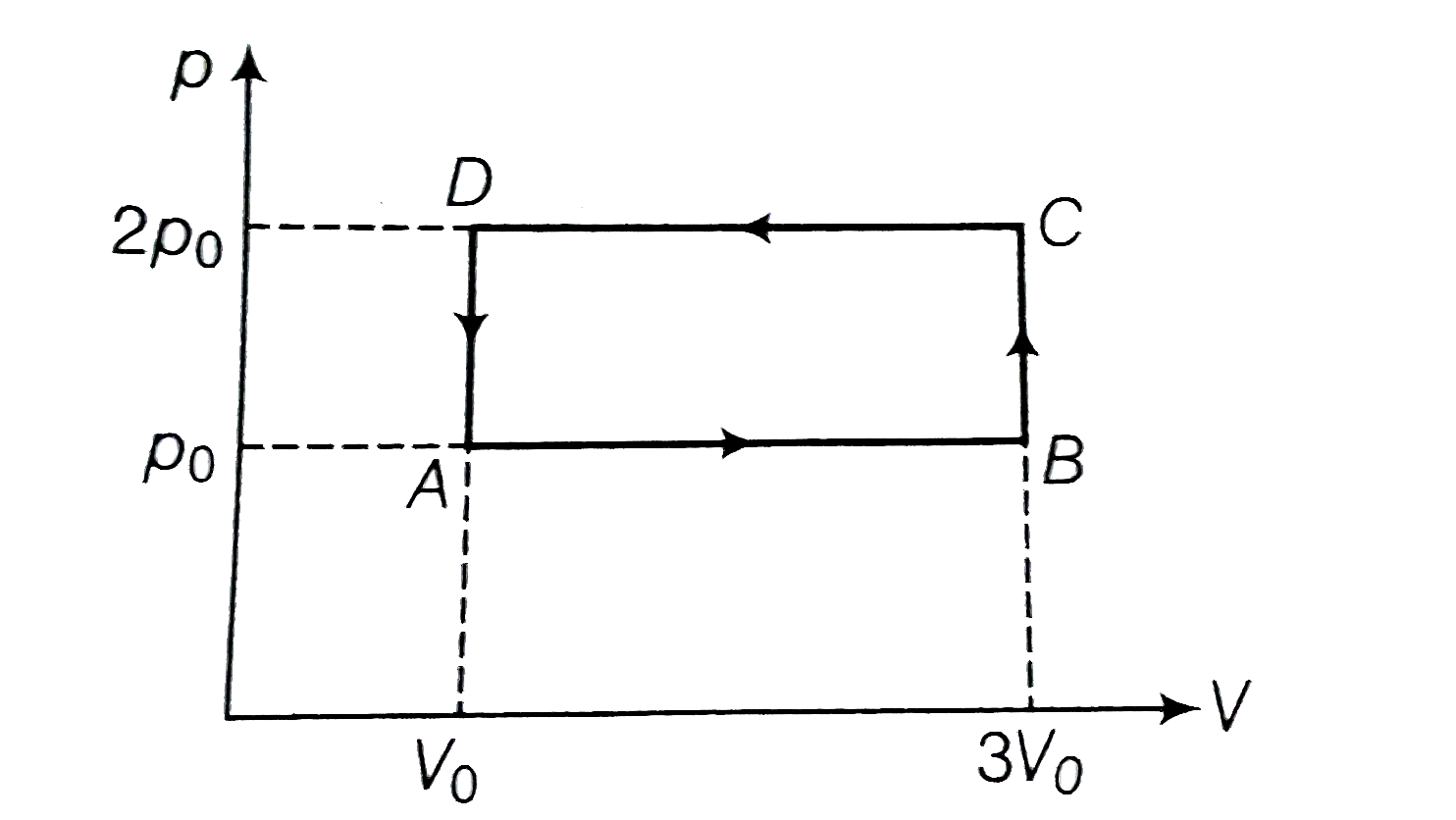
A−45RKB115RKC−52RKD2KAn ideal gas undergoes cyclic process ACBC as shown is given PV diagram
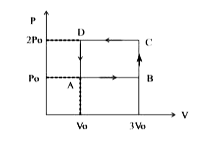
The amount of work done by the gas isA6PoVoB−2PoVoC+2PoVoD+4PoVo
One mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View SolutionOne mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then find the degree of freedom of gas
View SolutionAn ideal gas system undergoes an isothermal process, then the work done during the process is
View SolutionAn ideal gas system undergoes an isothermal process, then the work done during the process is
View SolutionOne mole of ideal gas goes through processP=2V21+V2. Then change in temperature of gas when volume changes from V=1m2 to 2m2 is :
View Solution