For a p-V plot, the slope of an adiabatic curve = x × slope of isothermal at the same point. Here x is :
Rλ−1
1λ
λ
1λ−1
The correct Answer is:C
To find the value of x in the relationship between the slopes of the adiabatic and isothermal curves on a p-V plot, we can follow these steps:
Step 1: Understand the Isothermal Process
In an isothermal process, the temperature remains constant. The equation governing this process is given by:
PV=constant
Differentiating this equation with respect to volume V gives us:
d(PV)=0⟹PdV+VdP=0
Rearranging this, we find:
dPdV=−PV
This expression represents the slope of the isothermal curve.
Step 2: Understand the Adiabatic Process
In an adiabatic process, there is no heat exchange with the surroundings. The relationship for an adiabatic process is given by:
PVλ=constant
where λ is the adiabatic constant. Differentiating this equation gives:
d(PVλ)=0⟹VλdP+PλVλ−1dV=0
Rearranging this leads to:
dPdV=−λPV
This expression represents the slope of the adiabatic curve.
Step 3: Relate the Slopes of the Two Processes
From the expressions derived, we have:
- Slope of isothermal process: dPdV=−PV
- Slope of adiabatic process: dPdV=−λPV
Step 4: Set Up the Relationship
We can set the slopes of the two processes equal to each other in the form:
slope of adiabatic=x×slope of isothermal
Substituting the expressions we derived:
−λPV=x(−PV)
Step 5: Solve for x
Cancelling the common terms −PV from both sides (assuming P and V are not zero):
λ=x
Thus, we find that:
x=λ
Final Answer
The value of x is equal to λ, the adiabatic constant.
---
In an isothermal process, the temperature remains constant. The equation governing this process is given by:
PV=constant
Differentiating this equation with respect to volume V gives us:
d(PV)=0⟹PdV+VdP=0
Rearranging this, we find:
dPdV=−PV
This expression represents the slope of the isothermal curve.
In an adiabatic process, there is no heat exchange with the surroundings. The relationship for an adiabatic process is given by:
PVλ=constant
where λ is the adiabatic constant. Differentiating this equation gives:
d(PVλ)=0⟹VλdP+PλVλ−1dV=0
Rearranging this leads to:
dPdV=−λPV
This expression represents the slope of the adiabatic curve.
From the expressions derived, we have:
- Slope of isothermal process: dPdV=−PV
- Slope of adiabatic process: dPdV=−λPV
We can set the slopes of the two processes equal to each other in the form:
slope of adiabatic=x×slope of isothermal
Substituting the expressions we derived:
−λPV=x(−PV)
Cancelling the common terms −PV from both sides (assuming P and V are not zero):
λ=x
Thus, we find that:
x=λ
The value of x is equal to λ, the adiabatic constant.
Similar Questions
Knowledge Check
In a p-V diagram for an ideal gas (Where , p is along y-axis and V is along X- axis) , the value of the ratio "slope pof adiabatic curve/ Slope of the isothermal curve"at any point will be (Where symbols have their usual meanings ).
A1B2CCp/CvDCv/CpThe slope of isothermal and adiabatic curves are related as
Aisothermal curve slope = adiabatic curve slopeBisothermal curve slope = γ×adiabatic slopeCadiabatic curve slope = γ× isothermal slopeDadiabatic curve slope = (1/2) × isothermal curve slopeSlope of normal to the curve y=x2−x and x=2 is
A−13B−17C−19D−111
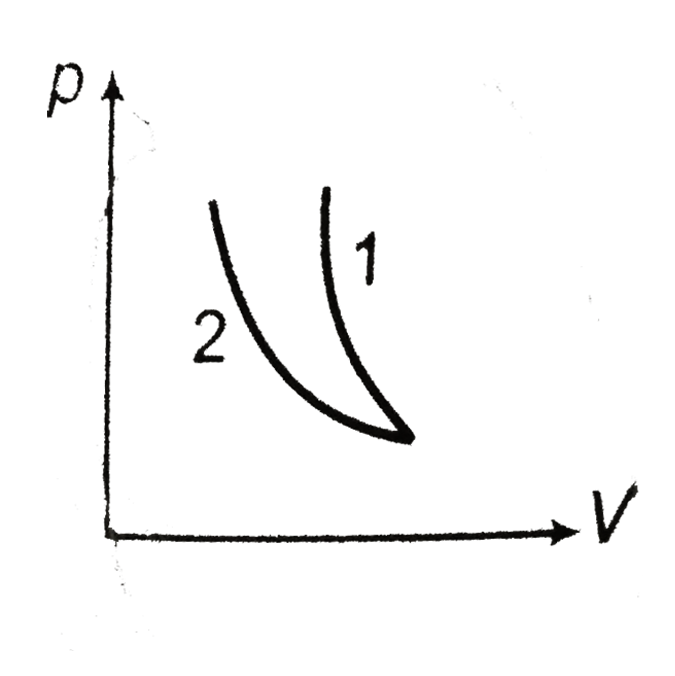
Assertion: Isothermal and adiabatic, two processes are shown on p-V diagram. Process-1 is aidabatic and process-2 is isothermal.
Reason: At a given point, slope of adiabatic process =γ×slope of isothermal process.
View SolutionA gas may expand either adiabatically or isothermally. A number of p−V curves are drawn for the two processes over different ranges of pressure and volume, it will be found that
(i) Two adiabatic curves do not intersect
(ii) two isothermal curves do not intersect
(iii) an adiabatic curve and an isothermal curve may intersect.
(iv) the magnitude of the slope of an adiabatic curve is greater thanthe magnitude of the slope of an isothermal curve
View SolutionIf slope of tangent to curve y=x3 at a point is equal to ordinate of point , then point is
View SolutionIn the plot of Λ and √C, the slope is
View SolutionThe ratio of slopes of adiabatic and isothermal curves is
View Solution
