Question

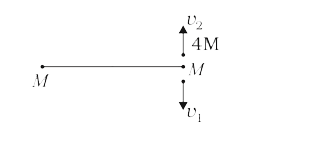
A satellite of mass $5M$ orbits the earth in a circular orbit. At one point in its orbit, the satellite explodes into two pieces, one of mass $M$ and the other of masses $4M$. After the explosion the mass $M$ ends up travelling in the same circular orbit, but in the opposite direction. After explosion the mass $4M$ is

Options

A. In a circular orbit
B. unbound
C. elliptical orbit
D. data is insufficient to determine the nature of the orbit.

Answer

B

Explanation

For circular orbit,
`(GMxx5M)/R^2 =(5Mv^2)/R rArr v^2=(GM)/R`
For mass M, to continue in its path in opposite dire
`(GMxxM)/R^2 =(Mv_1^2)/R rArr v_1^2=(GM)/R`
Angular momentum about centre should be conserved as there is no external torque on the system,
So , 5M x v x R = - `Mv_1xxR+4Mxxv_2xxR`
`rArr 5sqrt((GM)/R)=-sqrt((GM)/R)+4v_2 rArr v_2=3/2sqrt((GM)/R)`
Now ,
Total energy of the mass 4M,
`=1/2xx4Mxxv_2^2-(GMxx4M)/R`
`=(2Mxx9)/4(GM)/R - (4xxGM)/R =1/2 (GM^2)/r gt 0`
As T.E. > 0 so that mass 4M will become unbound