Assuming the earth to be a sphere of uniform density, the acceleration due to gravity
at a point outside the earth is inversely proportional to the square of its distance from the centre
at a point outside the earth is inversely proportional to its distance from the centre
at a point inside is zero
at a point inside is proportional to its distance from the centre
The correct Answer is:C
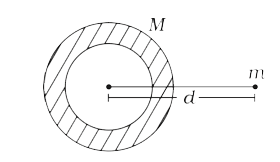
F=GMmd2
Similar Questions
Choose the correct alternative
(a)Acceleration due to gravity increase/decrease with increasing altitude.
(b) Acceleration due to gravity increase/decrease with increasing depth (assume the earth to be a sphere of uniform density).
(c ) Acceleration due to gravity is independer of mass of the earth/mass of the body.
(d) The formula −GMm(1r2−1r1) is more/less accurate than the formula mg(r2−r1) for the difference of potential energy between two points r2 and r1 distance away from the centre of earth.View Solution(a) Assuming the earth to be a sphere of uniform density, calculate the value of acceleration due to gravity at a point (i) 1600km above the earth, (ii) 1600km below the earth, (b) Also find the rate of variation of acceleration due to gravity above and below the earth's surface. Radius of earth =6400km,g9.8m/s2.
View Solution
Knowledge Check
- Question 1 - Select One
Assume the earth to be a sphere of uniform density the accleration due to gravity
Aat a point outside the earth is inversely proportional to the square of its distance from the centreBat a point outside the earth is inversely proportional to its distance from the centreCat a point inside is zeroDat a point inside is proportional to its distance from the centre. - Question 2 - Select One
Assuming the earth as a sphere of unifonn density. the acceleration due to gravity half way towards the centre of the earth will be
A0.75 gB0.50 gC0.25 gD0.125 g - Question 3 - Select One
Assuming earth to be a sphere of a uniform density, what is the value of gravitational acceleration in mine 100km below the earth's surface (Given R=6400km)
A9.66m/s2B7.64m/s2C5.06m/s2D3.10m/s2
Assuming the earth to be a sphere of uniform density, how much could a body weight at a height eqaul to radius of earth when it weight 250N on the surface of earth.
View SolutionIf earth is assumed to be a sphere of uniform density then plot a graph between acceleration due to gravity (g) and distance from the centre of earth.
View SolutionAssuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighd 250 N on the surface ?
View SolutionA body weight 250N on the surface. Assuming the earth to be a sphere of uniform mass density, how much would it weight half way down to the centre of earth
View SolutionAt the centre of earth the acceleration due to gravity is
View Solution
