Four uniform spheres, with masses mA=40kg,mB=35kg,mC=200kg , and mD = 50 kg, have (x,y) coordinates of (0, 50 cm), (0, 0), (–80 cm, 0), and (40 cm, 0), respectively. In unit-vector notation, what is the net gravitational force on sphere B due to the other spheres?
(2.6×10−5N)ˆj
(7.1×10−3N)ˆj
(3.7×10−7N)ˆj
(4.9×10−4N)ˆj
The correct Answer is:C
To find the net gravitational force on sphere B due to the other spheres (A, C, and D), we will follow these steps:
Step 1: Identify the positions and masses of the spheres
- Sphere A: mA=40kg at coordinates (0,50cm)
- Sphere B: mB=35kg at coordinates (0,0)
- Sphere C: mC=200kg at coordinates (−80cm,0)
- Sphere D: mD=50kg at coordinates (40cm,0)
Step 2: Calculate the gravitational force exerted on B by A
The gravitational force FAB between two masses is given by the formula:
F=Gm1m2r2
where G=6.67×10−11N m2/kg2 is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.
The distance rAB between A and B is:
rAB=√(0−0)2+(50−0)2=0.50m
Now, calculate the force:
FAB=GmAmBr2AB=6.67×10−1140×35(0.50)2
FAB=6.67×10−1114000.25=6.67×10−11×5600=3.74×10−7N
The direction of this force is downward (negative y-direction), so:
→FAB=−3.74×10−7^jN
Step 3: Calculate the gravitational force exerted on B by C
The distance rBC between B and C is:
rBC=√(−80−0)2+(0−0)2=0.80m
Now, calculate the force:
FBC=GmBmCr2BC=6.67×10−1135×200(0.80)2
FBC=6.67×10−1170000.64=6.67×10−11×10937.5=7.30×10−7N
The direction of this force is to the left (negative x-direction), so:
→FBC=−7.30×10−7^iN
Step 4: Calculate the gravitational force exerted on B by D
The distance rBD between B and D is:
rBD=√(40−0)2+(0−0)2=0.40m
Now, calculate the force:
FBD=GmBmDr2BD=6.67×10−1135×50(0.40)2
FBD=6.67×10−1117500.16=6.67×10−11×10937.5=7.30×10−7N
The direction of this force is to the right (positive x-direction), so:
→FBD=7.30×10−7^iN
Step 5: Calculate the net gravitational force on B
Now, we can find the net force →Fnet on sphere B by summing the forces from A, C, and D:
→Fnet=→FAB+→FBC+→FBD
→Fnet=(−3.74×10−7^j)+(−7.30×10−7^i)+(7.30×10−7^i)
→Fnet=−3.74×10−7^j+0^i
→Fnet=−3.74×10−7^jN
Final Answer
The net gravitational force on sphere B due to the other spheres is:
→Fnet=−3.74×10−7^jN
- Sphere A: mA=40kg at coordinates (0,50cm)
- Sphere B: mB=35kg at coordinates (0,0)
- Sphere C: mC=200kg at coordinates (−80cm,0)
- Sphere D: mD=50kg at coordinates (40cm,0)
The gravitational force FAB between two masses is given by the formula:
F=Gm1m2r2
where G=6.67×10−11N m2/kg2 is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.
rAB=√(0−0)2+(50−0)2=0.50m
FAB=GmAmBr2AB=6.67×10−1140×35(0.50)2
FAB=6.67×10−1114000.25=6.67×10−11×5600=3.74×10−7N
The direction of this force is downward (negative y-direction), so:
→FAB=−3.74×10−7^jN
The distance rBC between B and C is:
rBC=√(−80−0)2+(0−0)2=0.80m
FBC=GmBmCr2BC=6.67×10−1135×200(0.80)2
FBC=6.67×10−1170000.64=6.67×10−11×10937.5=7.30×10−7N
The direction of this force is to the left (negative x-direction), so:
→FBC=−7.30×10−7^iN
The distance rBD between B and D is:
rBD=√(40−0)2+(0−0)2=0.40m
FBD=GmBmDr2BD=6.67×10−1135×50(0.40)2
FBD=6.67×10−1117500.16=6.67×10−11×10937.5=7.30×10−7N
The direction of this force is to the right (positive x-direction), so:
→FBD=7.30×10−7^iN
Now, we can find the net force →Fnet on sphere B by summing the forces from A, C, and D:
→Fnet=→FAB+→FBC+→FBD
→Fnet=(−3.74×10−7^j)+(−7.30×10−7^i)+(7.30×10−7^i)
→Fnet=−3.74×10−7^j+0^i
→Fnet=−3.74×10−7^jN
The net gravitational force on sphere B due to the other spheres is:
→Fnet=−3.74×10−7^jN
Similar Questions
The masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centres is 100m, find the magnitude of the gravitational force between them.
View SolutionThe masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centres is 100 m, find the magnitude of the gravitational force between them.
View Solution
Knowledge Check
The centres of three spherical masses of 1 kg, 2 kg and 3 kg have co-orinates (4,0) m,(0,3)m and (-2,5)m respectively. What is the position vector of its centre of mass is terms of its x and y co-ordinates?
A→Rcm=2ˆi+3ˆjB→RcM=13ˆi+52ˆjCveRcm=≡−13ˆi+3.5ˆjD→rcm=23ˆi−53ˆjThree identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
A1.67×10−9(ˆi+ˆj)NB3.34×10−10(ˆi+ˆj)NC1.67×10−9(ˆi−ˆj)ND3.34×10−10(ˆi+ˆj)NTwo spheres, each of mass 625 kg, are placed with their centres 50 cm apart. The gravitational force between them is
A10.42 dyneB15.42 dyneC20.42 dyneD5.42 dyne
Two particles of masses 0.2 kg and 0.8 kg are separated by 12 cm. At which point from the 0.2 kg particle, gravitational field intensity due to the two particles is zero?
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionThree uniform spheres, each having a mass M=5kg and radius a=2.5m are kept in such a way that each touches the other two. Find the magnitude of the gravitational force in GN on any of the spheres due to the other two.
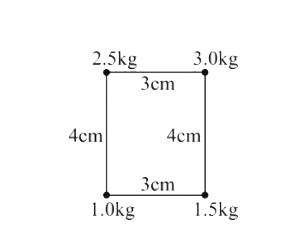
View SolutionFour point particles of masses 1.0 kg, 1.5 kg, 3.0 kg and 2.5 kg are placed at four corners of a rectangle of sides 4.0 cm and 3.0 cm as shown in the figure. The centre of mass of the system is at a point:
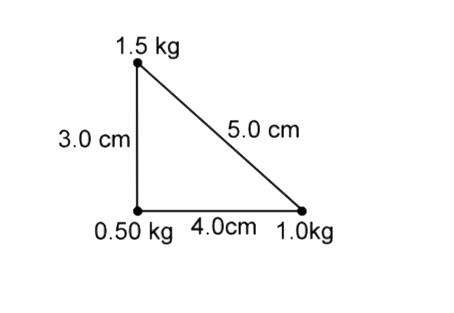
View SolutionThree particles of masses 0.5 kg, 1.0 kg and 1.5 kg are placed at the three corners of a right angled triangle of sides 3.0 cm, 4.0 cm and 5.0 cm as shown in figure. Locate the centre of mass of the system.
View Solution
