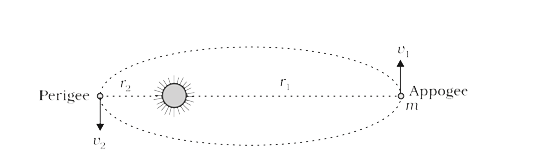
A planet of mass m moves along an ellipse around the Sun so that its maximum and minimum distances from the Sun are equal to $r_{1}$ and $r_{2}$ respectively. Find the angular momentum M of this planet relative to the centre of the Sun.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A planet of mass $m$ moves along an ellipse around the sun so that its maximum and minimum distance from the sun are equal to $r_{1}$ and $r_{2}$ respectively. Find the angular momentum of this planet relative to the centre of the sun. mass of the sun is $M$ .
A $m \sqrt{\frac{2 G M r_{1} r_{2}}{{(r_{1} + r_{2})}_{1}^{2}}}$
B $m \sqrt{\frac{2 G M r_{1}^{2} r_{2}^{2}}{{(r_{1} + r_{2})}_{1}^{2}}}$
C $m \sqrt{\frac{2 G M r_{1}^{2} r_{2}^{2}}{(r_{1} + r_{2})}}$
D $m \sqrt{\frac{2 G M r_{1} r_{2}}{(r_{1} + r_{2})}}$
A comet of mass m moves in a highly elliptical orbit around the sun of mass M the maximum and minium distacne of the comet from the centre of the sun are $r_{1}$ and $r_{2}$ respectively the magnitude of angular momentum of the comet with respect to the centre of sun is
A ${[\frac{G M_{1}}{r_{1} + r_{2}}]}^{1 / 2}$
B ${[\frac{G M m r_{1}}{r_{1} + r_{2}}]}^{1 / 2}$
C ${[\frac{r G M^{2} r_{1} r_{2}}{r_{1} + r_{2}}]}^{1 / 2}$
D ${[\frac{2 G M m^{2} r_{1} r_{2}}{r_{1} + r_{2}}]}^{1 / 2}$
A planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are $r_{1}$ and $r_{2}$ respectively. The period of revolution of the planet wil be proportional to :
A $r_{1}^{3 / 2}$
B $r_{2}^{3 / 2}$
C ${(r_{1} - r_{2})}_{1}^{3 / 2}$
D ${(r_{1} + r_{2})}_{1}^{3 / 2}$