Three particles, two with mass m and one with mass M, might be arranged in any of Rank the configuration according of the gravitational force on M, least to greatest.

1, 2, 3, 4
2, 1, 3, 4
2, 1, 4, 3
2, 3, 4, 1
The correct Answer is:B
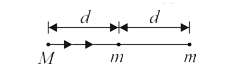
Fon M=GMmd2+GMm(2d)2=GMmd2[1+14]=54×GMmd2
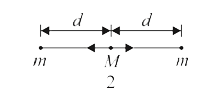
Fon M=GGMmd2−GMmd2=0
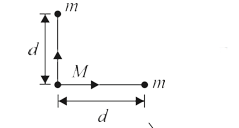
Fon M=GMm[(1d2)2+(1d2)2]12=√2GMmd2
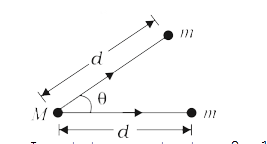
Fon M=GMmd2√2+2cosθ=√2(1+cosθ)GMmd2
Least to greatest : 2, 1, 3, 4
Similar Questions
A mass is at the center of a square, with four masses at the corners as shown.
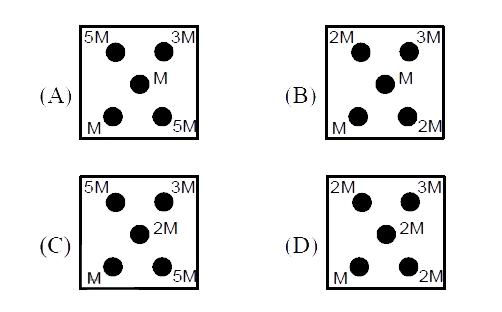
Rank the choices according to the magnitude of the gravitational force on the center mass.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View Solution
Knowledge Check
The figure shows four arrangements of three particles of equal masses. (a) Rank the arrangements accroding to the magnitude of the net gravitational force on the particlelabeled m, greatest first. (b) In arrangement 2, is the direaction of the net force closer of the line of length d or to theline of length D ?
A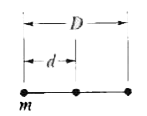 B
B C
C D
D
The figure shows four arrangement of three particles of equal masses. Rank the arrangement according to the magnitude of the net gravitational force on the particle m, greatest first.
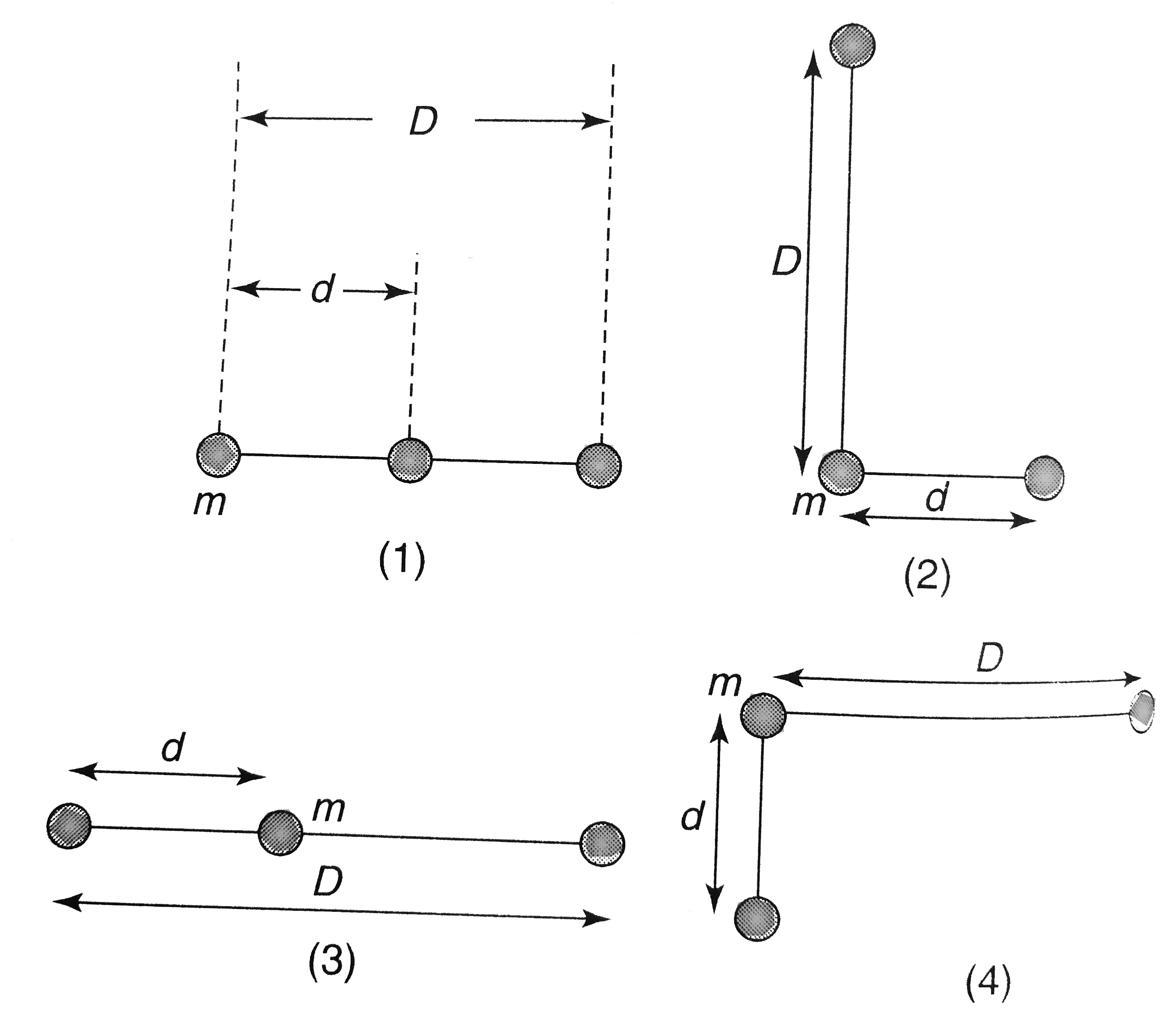 A1, tie of 2 and 4, then 3B1,4,3,2C2,3,4,1D4,3,1,2
A1, tie of 2 and 4, then 3B1,4,3,2C2,3,4,1D4,3,1,2A mass is at the centre of a square, with four masses at corners as shown
Rank the choice according to the magnitude of the gravitational force of the centre mass


Rank the choice according to the magnitude of the gravitational force of the centre mass-AFA=FB<FC=FDBFA>FB<FD<FCCFA=FB>FC=FDDnone
Consider the situation as shown in the following diagrams. Find net gravitational force on the particle of mass m.
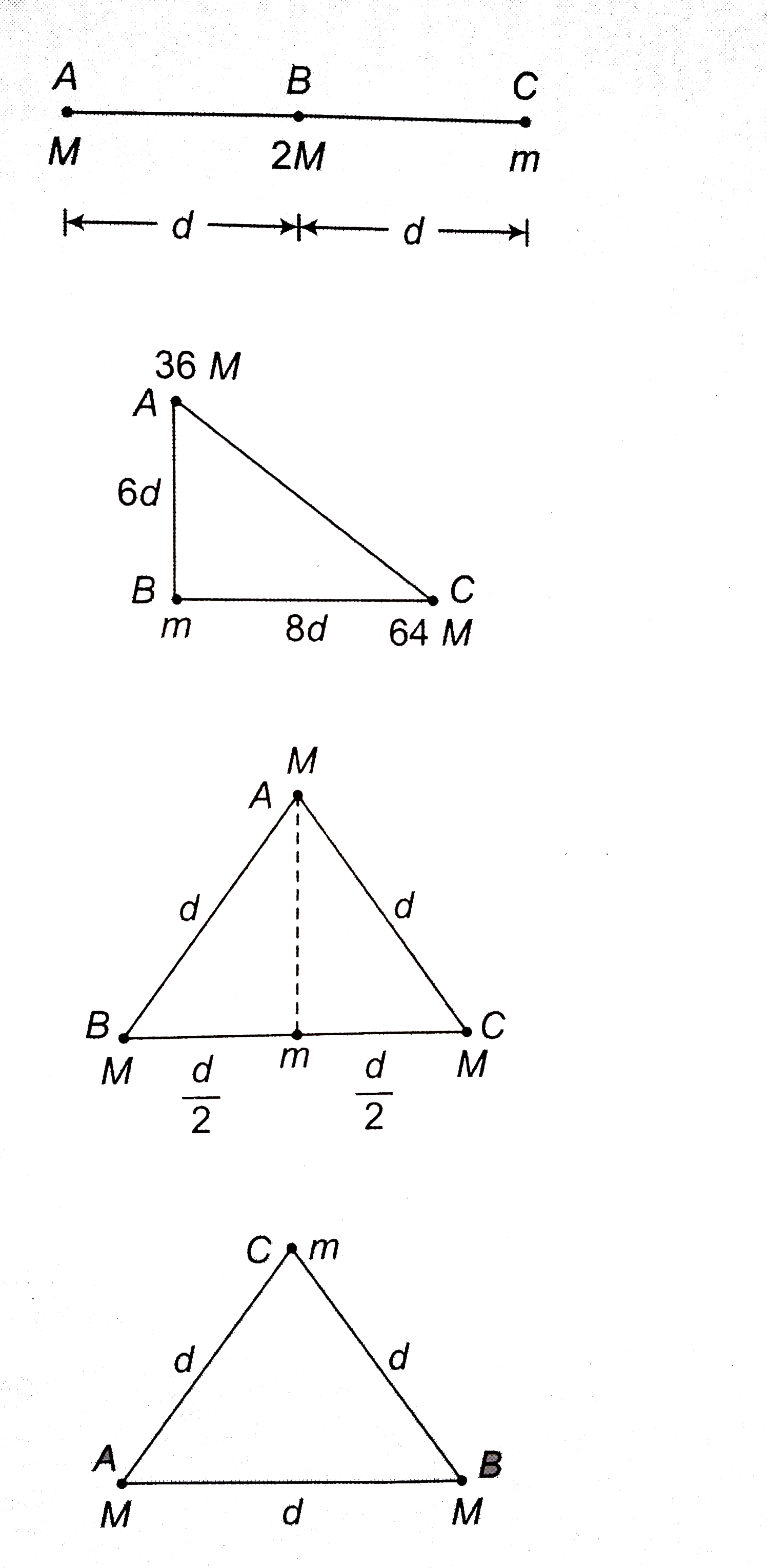

View SolutionIf two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View SolutionThe reduce mass of two particles having masses m and 2 m is
View SolutionA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
View SolutionThree uniform spheres each of mass m and diameter D are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
View Solution

