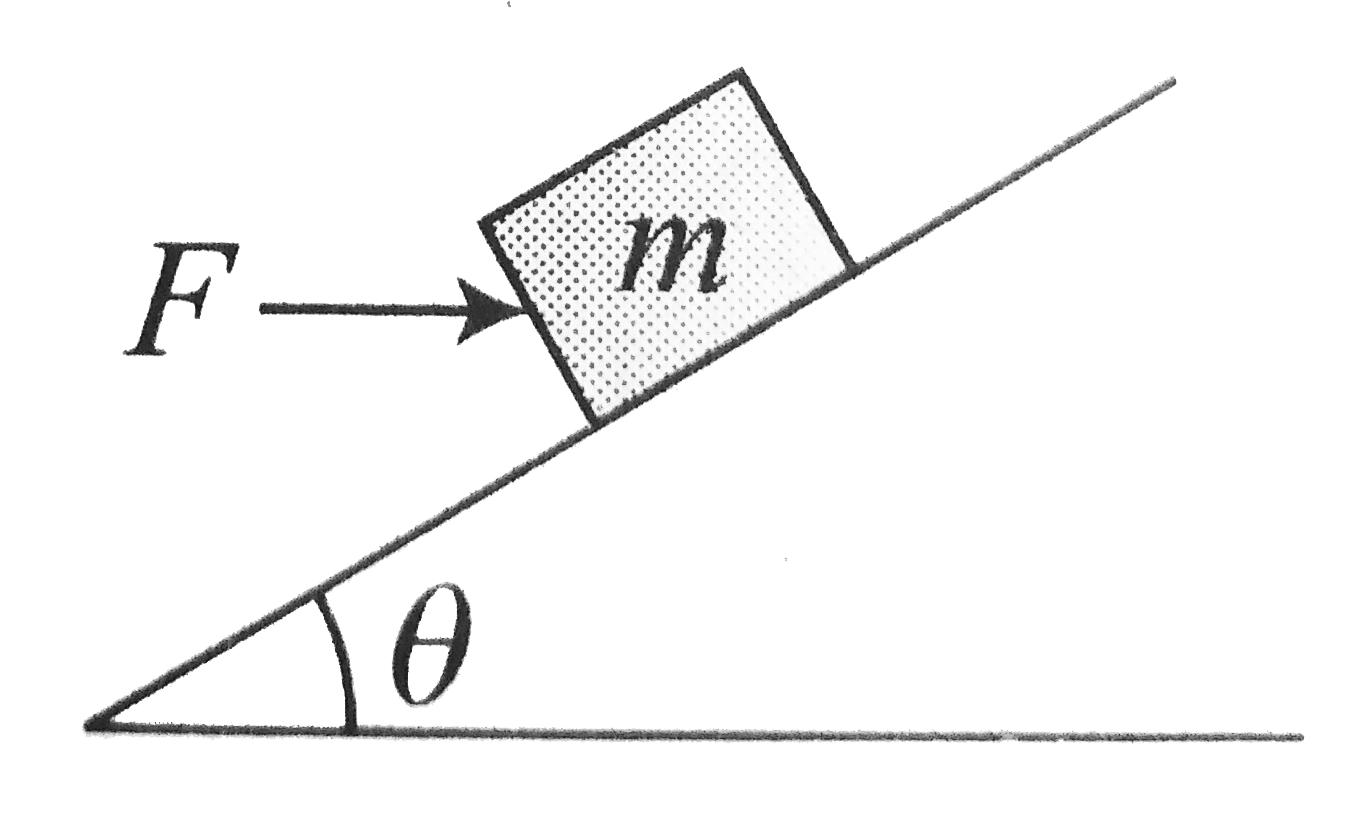
A small block of mass of 0.1kg lies on a fixed inclined plane PQ which makes an angle θ with the horizontal. A horizontal force of 1N acts on the block through its centre of mass as shown in the figure. The block remains stationary if ( take g=10m/s2)
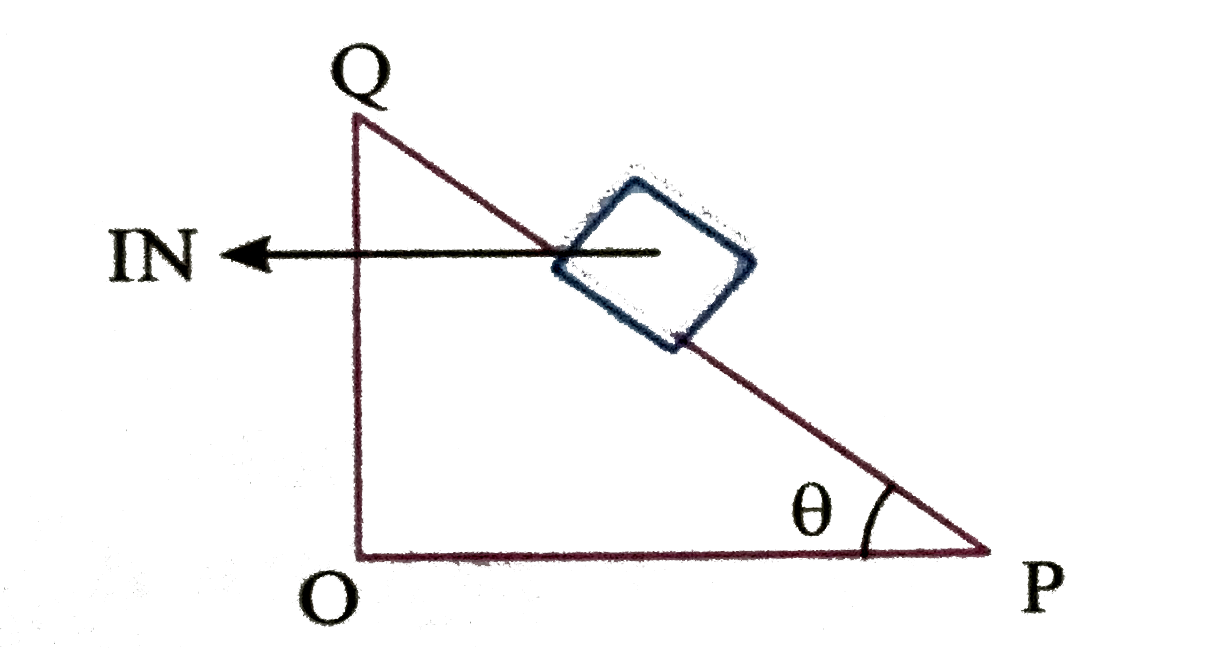
θ=45∘
θ>45∘ and a frictional force acts on the block towards
θ>45∘and a frictional force acts on the block towards
θ<45∘ and a frictional force acts on the block towards Q
The correct Answer is:A, C
f = 0, If mgsinθ=Fcosθ⇒θ=45∘
f towards Q, mgsinθ>Fcosθ⇒θ>45∘
f towards P, mgsinθ<Fcosθ⇒θ≤45∘
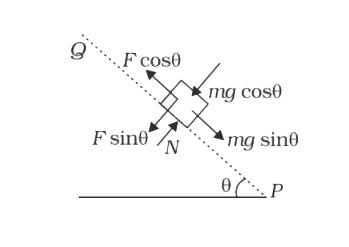
Similar Questions
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of 4kg slides down an inclined plane which makes an angle θ=60∘ with the horizontal. The co-effcient of friction between the block and the plane is μ=3/4. The force exerted by the block on the plane is (g=10m/s2)
View Solution
Knowledge Check
A small block of mass of 0.1 kg lies on a fixed inclined plane PQ which makes an angle θ with the horizontal. A horizontal force of 1N acts on the block through its centre of mass as shown in figure.
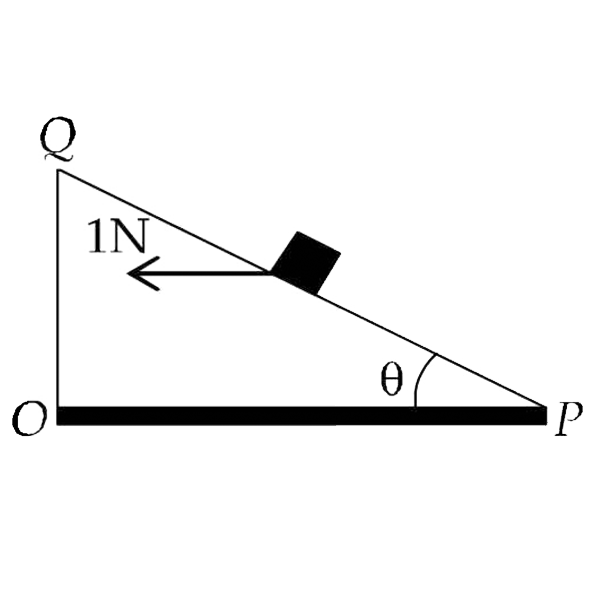
The block remains stationary if (take g=10m/s2)Aθ=45∘Bθ>45∘ and a frictional force acts on the block towards P.Cθ>45∘ and a frictional force acts on the block towards Q.Dθ<45∘ and a frictional force acts on the block towards Q.A small block of mass of 0.1 kg lies on a fixed inclined plane PQ which makes an angle θ with the horizontal. A horizontal force of 1 N acts on the block through its center of mass as shown in the figure. The block remains stationary if (take g = 10 m/s2)
 Aθ=45∘Bθ>45∘ and a frictional force acts on the block towardsP.Cθ>45° and a frictional force acts on the block P towards Q.Dθ<45° and a frictional force acts on the block towards Q.
Aθ=45∘Bθ>45∘ and a frictional force acts on the block towardsP.Cθ>45° and a frictional force acts on the block P towards Q.Dθ<45° and a frictional force acts on the block towards Q.A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ
A horizontal force F acts on the block of mass m and the block remains stationary, thr value of friction force is.

View SolutionA block of mass m rests on a fixed incline plane of inclination θ with horizontal Assume friction is large enough to make the block stationary. Then choose correct alternative (s)
View SolutionA block is kept on a rough horizontal surface. A variable horizontal force is acting on the block as shown in the figure. At t=0, block is at rest. Kinectic energy of block at t=5sec will be (g=10m/s2)
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA horizontal force acting on a block of mass m which is placed on an inclined plane (as shown in the figure). What is the normal reaction N on the block?
View Solution
